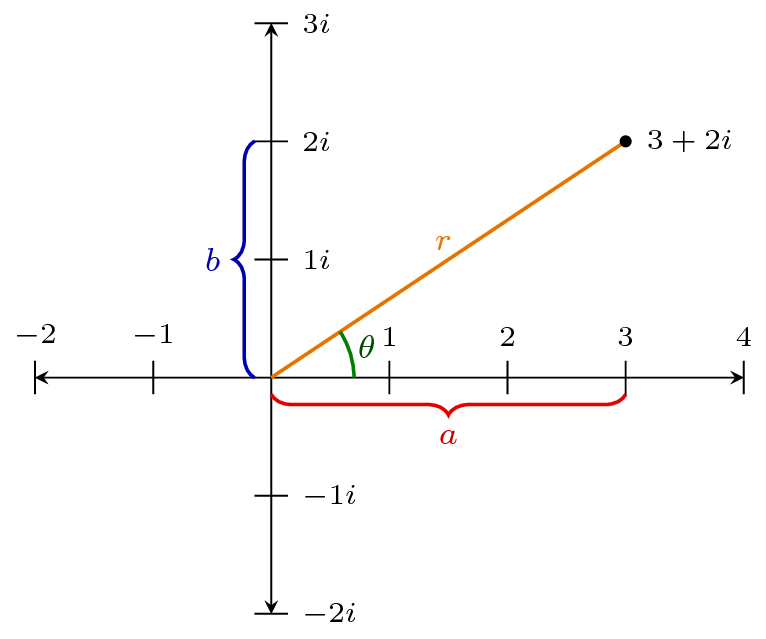Förkunskaper

Innehåll

Innan kursen påbörjas förväntas studenten ha vissa förkunskaper. Några bitar som ska kunnas men ofta behövs repeteras är:

• Imaginära tal
• Differentialekvationer
• Exempel: Första ordningens system
• Linjärisering

Imaginära tal

Ett imaginärt tal består av en realdel och en imaginärdel. De två vanligaste representationerna för imaginära tal är rektangulär form och polär form, se figur.

Båda representationer har sina fördelar. Rektangulär form är smidig vid addition av imaginära tal, och polär form har fördelen att vi direkt kan räkna ut både belopp (storlek) och argument (vinkel):

\begin{align} |z| & = \sqrt{a^2+b^2}=r \nonumber \\\arg(z) & = \arctan{\frac{b}{a}}~=\theta \nonumber \end{align}

Differentialekvationer

I denna kurs behandlar vi linjära differentialekvationer på formen:

\begin{align} \frac{d^ny}{dt^n} &+ a_1 \frac{d^{n-1}y}{dt^{n-1}} + \ldots + a_n y \nonumber \\ &= b_0 \frac{d^{m}u}{dt^{m}} + b_1 \frac{d^{m-1}u}{dt^{m-1}} + \ldots + b_m u \nonumber \end{align}

Lösningen beräknas som summan av en homogen lösning¹ (även kallad allmän lösning) och en en partikulärlösning²:

Homogen lösning

Den homogena lösningen är lösningen till motsvarande homogena differentialekvation, och fås från lösningen till det karakteristiska polynomet: \begin{equation} (\lambda^n + a_1 \lambda^{n-1} + \ldots + a_n) = 0 \nonumber \end{equation} Denna ekvation har $n$ stycken rötter, som antingen är:

• reella tal: $\lambda = p$
• komplexa talpar: $\lambda_1 = a+bi,~~\lambda_2 = a-bi$

Rötterna ger oss den homogena lösningen som:

där $\lambda_j$ är den $j$:te roten och $\alpha_j$ är koefficienter. Notera att

• Om $\lambda_j$ har positiv realdel så växer $y_h$ obegränsat
• Om imaginärdelen är $0$ blir bidraget rent exponentiellt.
• Ett komplext talpar ger oscillationer (tänk på Eulers formel). Ju större imaginärdel desto mer kommer det osciellera.

Partikulärlösning

Partikulärlösningen hittas ofta genom att man ansätter att en lösning ska ha en viss form, för att därefter lösa ut konstanterna.

Exempel: första ordningens system

Lös följande differentialekvation: \begin{align}\label{eq:ex1} 10 \dot y(t) &+ y(t) = 2 u(t) \end{align} med insignal $u(t) = 1$ då y(0) = 0.

Den homogena lösningen fås av: \begin{align} \dot y(t) &+ \frac{1}{10}y(t) = 0 \nonumber
\end{align} Koeffecienteren är således $a_1 = \frac{1}{10}$ och det karakteristiska polynomet ger:

För partikulärlösningen ses direkt lösningen $ y_p = 2 $. Från detta vet vi att differentialekvationen har formen $ y(t) = Ce^{-1/10t} + 2$. Den sista konstanten löser vi ut från begynnelsevilkoret:

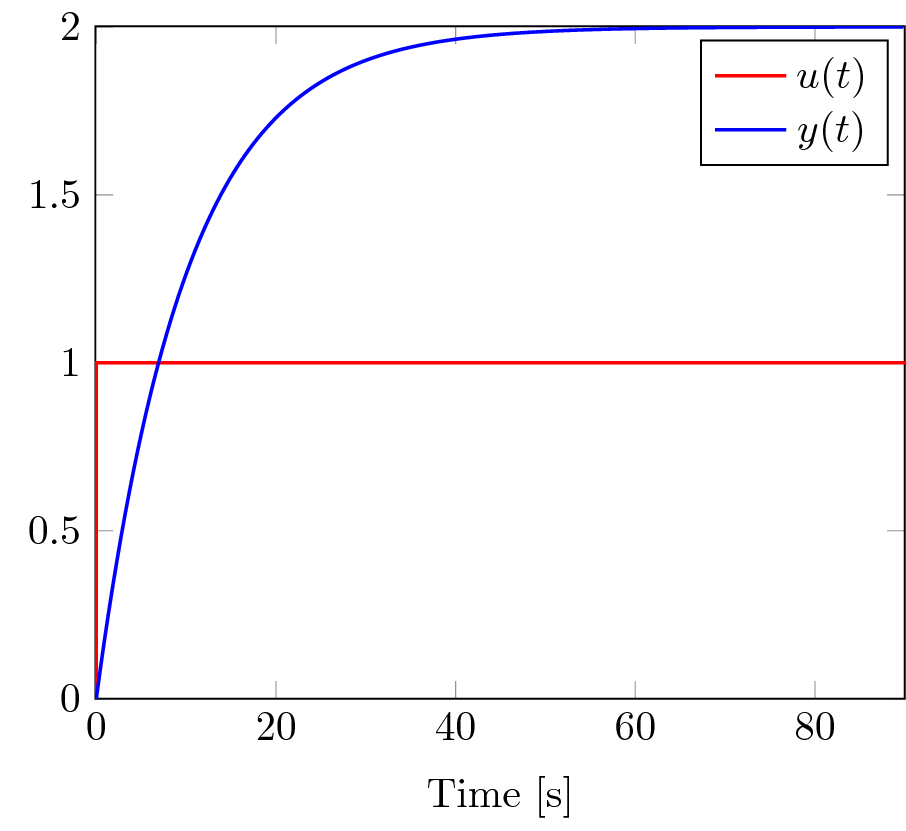
Svar: $ y(t) = 2\left(1-e^{-1/10t} \right)$

Linjärisering

I verkligheten är de flesta system icke-linjära, men i denna kurs behandlar vi enbart linjära system. För att uppskatta en linjär funktion från från en icke-linjär använder vi oss av linjärisering.