Dämpning, Rotort

Rotort

Vi har tidigare (uppgift 3.1, exempelsamling) sett hur storleken på återkopplingen kan påverka polernas placering. Nu ska vi mer formellt titta på detta samband med hjälp av rotorter1. Rotorten är ett verktyg som vi har och kan använda bland annat när vi fattar reglerdesignbeslut.

I praktiken ritar man inte själv ut rotorten utan man låter en dator göra det. I Matlab görs detta med kommandot:

  rlocus(sys)

Steg: Så ritar du en rotort

Vi ritar ut varje pols förflyttning som en “gren”. Totalt finns $n$ st grenar.

  • Skriv om ditt polpolynom på formen $P(s) + KQ(s) = 0$ där K är varibeln som du vill variera
  • Ändpunkter: Rötterna till $Q(s)$ motsvarar $K = \infty$ [$m$ st]
  • Startpunkter: Rötterna till $P(s)$ motsvarar $K = 0$ [$n$ st]
  • $a_1 = \sum{startpunkter}$, $b_1 = \sum{\ddot andpunkter}$
  • Asymptoter: Om $m<n$ kommer $(n-m)$ grenar gå mot oändligheten. \ De utgår från $-\frac{a_1-b_1}{n-m}$ i riktningarna $\frac{\pi}{n-m}(1+2k)$ då $k=0,\ldots,n-m-1$
  • Vi skär den imaginära axeln då $P(i\omega) + KQ(i\omega) = 0$
  • De delar av reella axeln med ett udda antal reella start- eller ändpunkter till höger, tillhör rotorten.

Exempel: skriv om polekvationen

Rotorten härleds genom att betrakta polekvationen under olika återkopplingar. Anta att vi återkopplat vårt system

med regulatorn $F(s) = k_P + \frac{1}{s}k_I.$ Polekvationen blir då: \begin{align} 1 + F(s)G(s) &= 0 \implies\nonumber \\ s^3+10s^2 + (29+20k_P)s + 20k_I &= 0 \nonumber \end{align} Vi är intresserade av hur polernas placering beror på $k_P$ och $k_I$. Vi börjar med att kolla på hur de beror på $k_P$. Därför delar vi upp ekvationen i två polynom:

Vi kan nu skriva ekvationen som: \begin{equation}\label{eq:root_locus1} P(s) + K \cdot Q(s) = 0 \end{equation}

Sätt $k_I=1$. Vi identifierar från detta:

  • Startpunkter: -1,-4,-5
  • Ändpunkter: 0
  • Asymptoter: 2 st, utgår från $-5$ och har riktningarna $\pi/2$ och $3\pi/2$.
  • Delar av reela axeln som tillhör rotorten är $[-5,-4]$ och $[-1,0]$

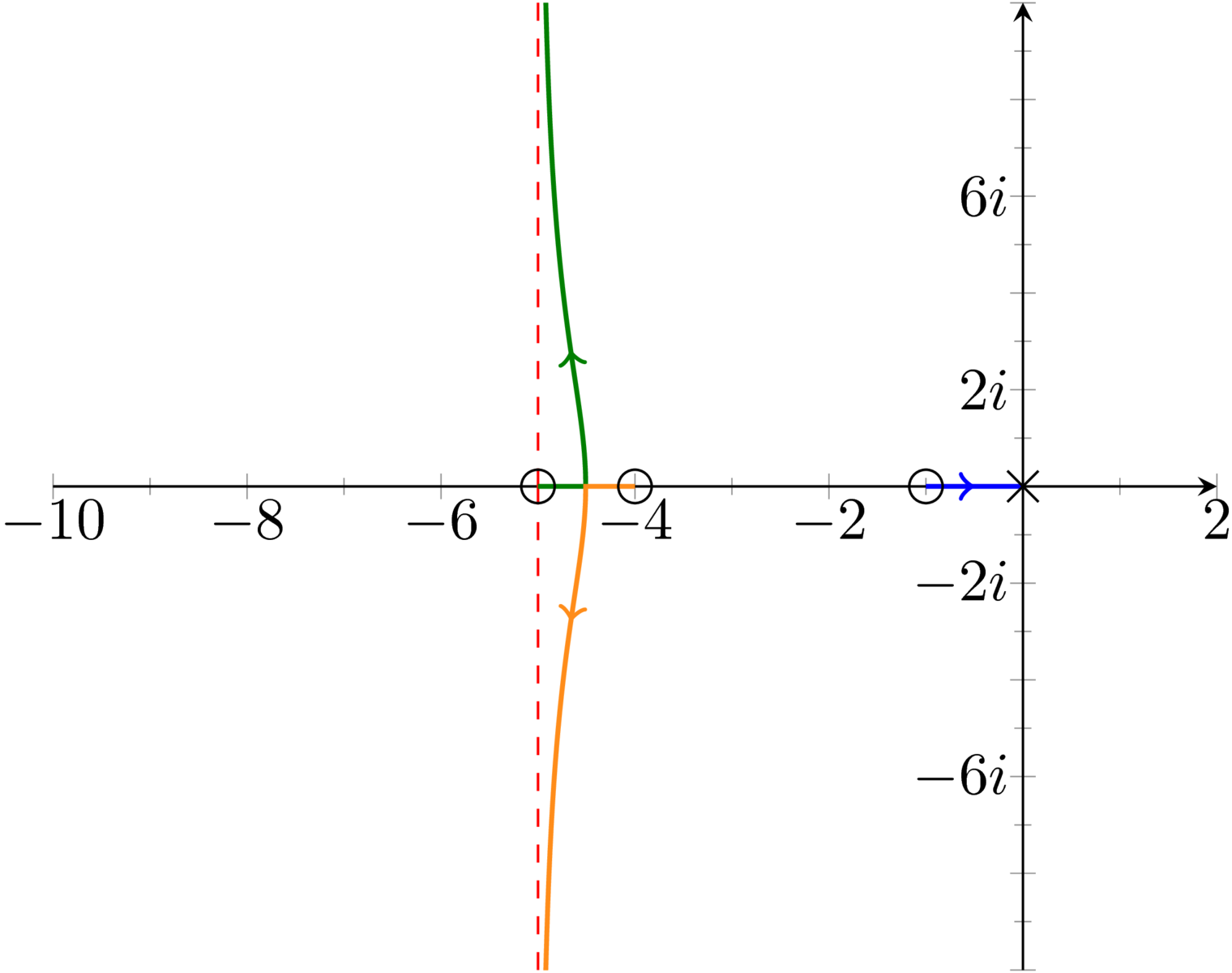
Resultatet visas i figur nedan.

Figure: Root locus plot of the system.

Övningsuppgifter

3.33, 3.5a, 3.6abd

  1. https://en.wikipedia.org/wiki/Root_locus ↩