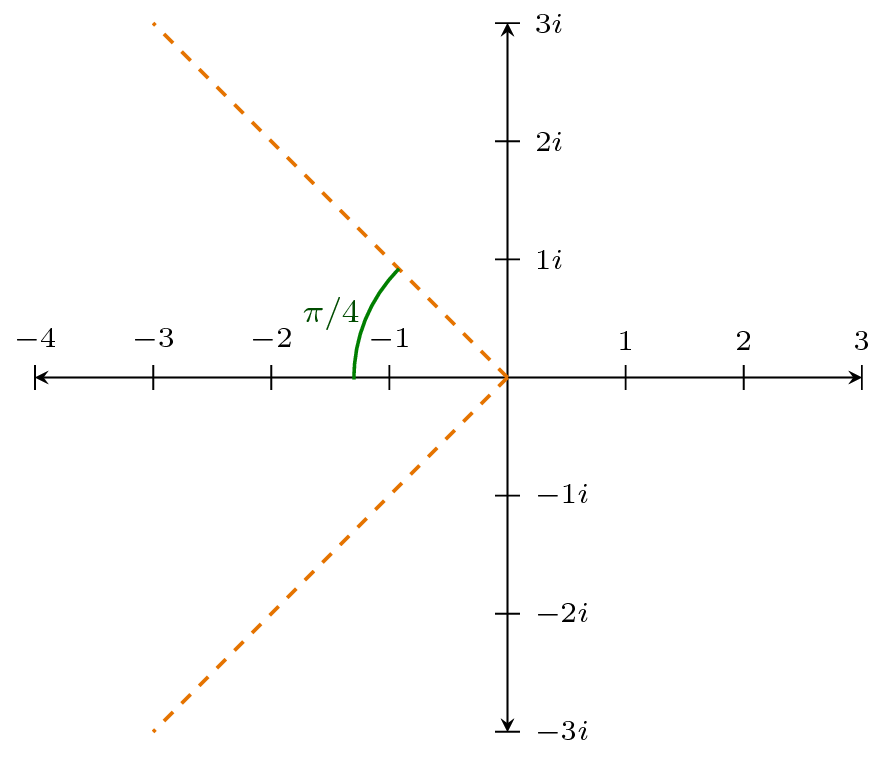Terminologi, Stegsvar & Poler

Innehåll

• Dynamiska system/Differentialektationer
• Poler och nollställen - varifrån kommer de och hur spelar de roll?
• Stegsvar - hur kan vi relatera ett system till dess stegsvar?

Laplacetransformen

I klassisk reglerteknik löser vi ofta problem i frekvensdomänen. Med hjälp av Laplacetransformen¹ får vi ut överföringsfunktionen för systemet:

\begin{align} Y(s) = \underbrace{\frac{b_0s^m + b_1s^{m-1} + \ldots + b_m}{s^n + a_1 s^{n-1} + \ldots +a_n}}_{G(s)} U(s) \end{align} Rötterna till täljaren hos överföringsfunktionen $G(s)$ är systemets nollställen, och rötterna till nämnaren är systemets poler. Notera hur polerna motsvaras av lösningarna till den karakteristiska ekvationen.

Exempel: första ordningens system

\begin{align*} T \dot y(t) &+ y(t) = K u(t) \\ &\implies G(s) = \frac{b}{s+a} \end{align*} Har en reell pol i $s=-a$

Exempel: andra ordningens system

Systemet givet av: \begin{align*} \ddot y(t) &+ 2\zeta \omega_0 \dot y(t) + \omega_0^2 y(t) = \omega_0^2 u(t) \\ &\implies G(s) = \frac{\omega_0^2}{s^2+2\zeta\omega_0 s + \omega_0^2} \end{align*}

har två poler som ligget i $s = \omega_0(-\zeta \pm i\sqrt{1-\zeta^2})$. Polerna kan anta reella vörden eller bilda ett komplext talpar beroende på värdet på den relativa dämpningen $\zeta$.

Pol/nollställe-diagram

Beteendet hos ett dynamiskt system kan beskrivas med positionen av dess poler och nollställen. Om vi känner till placeringen av polerna och nollställena kan vi avgöra stabiliteten hos systemet, och även om det oscillerar, är snabbt, m.m. Några tumregler är:

• Positiv realdel ger ett instabilt system

• En pol i origo har en effekt motsvarande en integrator.

• De poler som är närmast origo kommer att dominera över de långt borta. Alternativt kan vi uttrycka detta som att snabba poler (stor realdel) försvinner snabbare än långsamma poler (liten realdel).
• Den odämpade egenfrekvensen $\omega_0$ mäts från vinkeln mellan realaxeln och polen. Man vill oftast att polerna ska ligga innanför en kon enligt figur för att systemet inte ska bete sig för oscillerande.

Stegsvar

Stegsvar kan användas både för att karakterisera beteendet hos ett system, och även för att identifiera parametrar hos ett okänt system. Svegsvaret är den utsignal vi får när vi som insignal ger:

När vi betraktar stegsvaret kan vi observera flera karaktärsdrag i svaret, bland dessa kan nämnas:

• stabilitet
• oscillationer
• slutvärde
• översläng
• tidsfördröjning
• snabbhet Med hjälp av dessa kan vi lista ut hur ett system bör matcha med pol/nollställe-diagram.

Övningsuppgifter

2.5, 2.10, 2.11