| INTRO |
5A:2
 5A
5A
Trig.formler
5A.2 Trigonometriska funktioner (forts.)
Den viktigaste geometriska representationen av de trigonometriska funktionerna är naturligtvis deras grafer.Som påpekades i samband med de trigonometriska formlerna 2-3 innehåller graferna en massa information som bl.a. kan formuleras som formler.
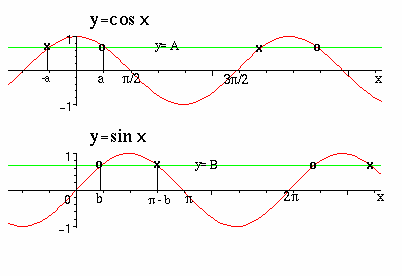
Här nedan är graferna för sinus och cosinus.
Lägg samtidigt märke till hur dessa kurvor skär linjer av typ y=konstant.
Detta har nämligen betydelse i samband med trigonometriska ekvationer.
Sinus- och cosinusfunktionerna har oändligt många nollställen. Detta är en egenskap, som exempelvis inga polynom har. Att hantera oändligt många nollställen innebär en speciell svårighet.
Nollställena för sinusfunktionen är de tal x = n som
erhålles då n antar alla heltalsvärden, dvs n = 0, ±1, ±2, ±3, osv.
| OBS, I fortsättningen i detta avsnitt underförstår vi att uttryck som innehåller n står för den mängd som erhålles då n antar alla heltalsvärden. |
Cosinusfunktionen har nollställena x = /2 + n
Med stöd av graferna ovan och kommentarerna till höger kan man ställa upp följande regler för lösningar av ekvationerna:

cos x = cos a har lösningen:

Kommentarer.
Observera hur lösningarna till ekvationerna cos x = cos a och sin x = sin a
beror av symmetrierna hos kurvorna
y = cos x resp. y = sin x.
I cosinusfallet ser man att de oändligt många lösningarna bildar två sviter
med x-värden med inbördes
differenser på 2:
En som utgår från x=a (o-punkterna) och en som utgår från x=-a (x-punkterna).
På motsvarande sätt bildar lösningarna till sin x = sin b två sviter som utgår från
x=b (o-punkterna) resp. x = - b (x-punkterna).
![]()
![]()