| INTRO |
 |
 |
 |
 |
 |
 |
|
|
|
|
 |
 |
 |
4A:1
4A
Ex 4.1
4A : Logaritmer.
Logaritmer och exponentialfunktioner är varandras spegelbilder:
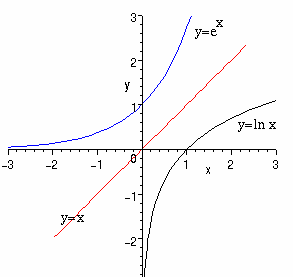
Speglingen sker i linjen y = x , vilket innebär att om punkten (x,y) ligger på grafen för y=ex så ligger spegelpunkten (y,x) på grafen för y = ln x.
I det här avsnittet måste man kunna:
som exempelvis medför att
som motiverar likheterna
samt definitionen av logaritmen med bas a (a > 0):
med specialfallet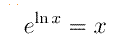 
då basen är talet e:
.
| ln x är alltså det tal som e skall upphöjas till för att man skall få x |
varav bl.a. följer att ln 1 = 0 och ln e = 1.
Observera också att
är nödvändigt för att ln x ( och alla andra logaritmer) skall vara definierad.
Kommentarer.
Byte mellan x och y i en ekvation, exempelvis
från (1) y = 2x+1 till (2) x = 2y +1, dvs y = (x-1)/2
ger alltid två kurvor vars grafer är varandras spegelbilder i linjen y=x .
Kontrollera gärna detta för det givna exemplet!
Byte mellan x och y i y = ex ger
ekvationen x = ey, som alltså definierar
samma kurva som y = ln x.
Jämför likheten eln x = x nertill på sidan till vänster.
| Dessa s.k. potensregler liksom
logaritmdefinitionerna måste naturligtvis inläras noggrant! |
Alla de 17 givna decimalerna för e behöver dock inte läras in.
e är inte bara ett irrationellt tal utan även ett transcendentalt tal, dvs är inte ett nollställe till ett polynom med heltalskoefficienter (visades av Hermite 1873 ).
Eftersom e är irrationellt förekommer ingen periodicitet i decimalutvecklingen, trots att man
kan luras att tro det efter de 9 första decimalerna.