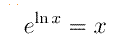print4A

4A : Logaritmer.

Logaritmer och exponentialfunktioner är varandras spegelbilder:

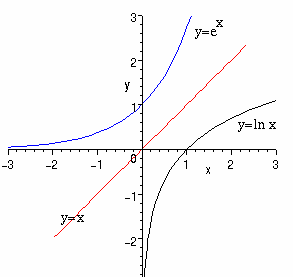Speglingen sker i linjen y = x , vilket innebär att om punkten (x,y) ligger på grafen för y=e^x så ligger spegelpunkten (y,x) på grafen för y = ln x.

I det här avsnittet måste man kunna:

som exempelvis medför att

2³·2^-2 = 2^3-2 =2¹ = 2,

som motiverar likheterna

8⁴ = (2³)⁴ = 2^3·4 = 2¹²,

samt definitionen av logaritmen med bas a (a > 0):

med specialfallet

då basen är talet e:

ln x är alltså det tal som e skall upphöjas till för att man skall få x

varav bl.a. följer att ln 1 = 0 och ln e = 1.

Observera också att

x > 0

är nödvändigt för att ln x ( och alla andra logaritmer) skall vara definierad.

4A : Logaritmer (forts).

Med hjälp av logaritmens definition och av potenslagarna kan man härleda följande viktiga logaritmlagar (de formuleras här för ln, men gäller för alla logaritmer):

En typisk användning av logaritmer är att applicera dem på bägge led i en ekvation där x förekommer i exponenten.
Ofta kan man då lösa ekvationen som i Ex 4.1a nedan:

Om det däremot förekommer något + eller - i ekvationen är logaritmen verkningslös. Det finns nämligen ingen formel som förenklar uttryck av typen ln(a+b).

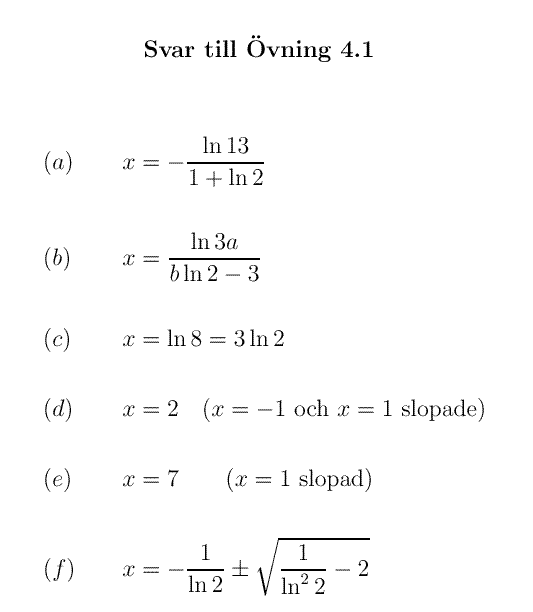
I samband med logaritmer uppstår ofta definitionsmängdsproblem (som för kvadratrötter) vilket fordrar att erhållna rötter prövas i ursprungsekvationen: