| INTRO |
5A:1
 5A
5A
Trig.formler
5A : Trigonometriska funktioner.
Till att börja med bör man vänja sig vid vinkelmåttet radianer så att översättningen mellan radianer och grader sker utan bekymmer:
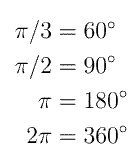
Sedan måste man behärska värdena för sinus och cosinus (och tangens, men just nu koncentrerar vi oss på sin och cos) för det fåtal vinklar som ger enkla värden på dessa funktioner.
Nedanstående figur ger indirekt information om värdena på sin, cos och tan
för vinklarna /6,
/4 och
/3.
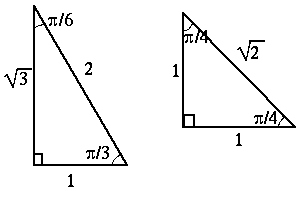
Och så är det då alla formler.
Länken 'Trig.formler' till vänster leder till en formelsamling.
Mängden formler kan verka avskräckande.
Men man kan hitta mönster som gör att inlärningen sker
lättare:
- 1. Trigonometriska ettan brukar vara den första formeln som fastnar.
- Formlerna 2 - 3 ger viktig information om funktionernas
perioder och symmetrier.
Dessa formler innehåller information som också finns nedlagd i funktionernas geometriska definition (m.hj.a. enhetscirkeln) eller i funktionernas grafer (se också nästa sida). Kommer man alltså ihåg hur graferna ser ut så har man nästan formlerna 2-3 till skänks.
M.hj.a. dessa formler kan man också lösa problem där det gäller att bestämma sinus och cosinus av kända vinklar som dock ligger utanför intervallet 0 < v <.
Ex. cos(14
/3) = cos(4
+ 2
/3)
= cos(2/3) = - cos(
- 2
/3)
= - cos(/3) = -1/2.
Övning 5.1 ger en del träning på sådant.
Kommentarer.
En fördel med radianmåttet är att formeln för
cirkelns båglängd blir enkel:
L= v·R , där L är båglängden, v motsvarande medelpunktsvinkel i radianer samt R cirkelns radie.
Eller: Vinkelns värde (radianer) = motsvarande båglängd i enhetscirkeln (som ju har R=1).
Även andra vinklar har sinus- och cosinusvärden som är uttryckbara med kvadratrötter.
Dit hör bl.a.
Men detta är inget som man normalt belastar minnet med.