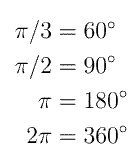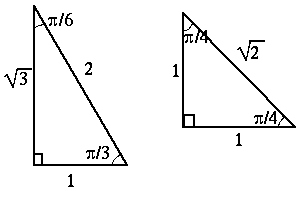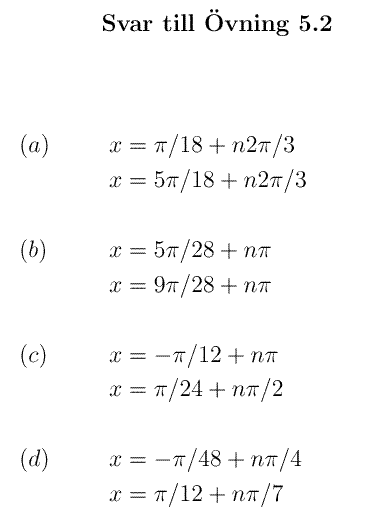5A : Trigonometriska funktioner.

Till att börja med bör man vänja sig vid vinkelmåttet radianer så att översättningen mellan radianer och grader sker utan bekymmer:

Sedan måste man behärska värdena för sinus och cosinus (och tangens, men just nu koncentrerar vi oss på sin och cos) för det fåtal vinklar som ger enkla värden på dessa funktioner.

Nedanstående figur ger indirekt information om värdena på sin, cos och tan för vinklarna /6, /4 och /3.

Och så är det då alla formler.
Länken 'Trig.formler' till vänster leder till en formelsamling.
Mängden formler kan verka avskräckande. Men man kan hitta mönster som gör att inlärningen sker lättare:

• 1. Trigonometriska ettan brukar vara den första formeln som fastnar.

• Formlerna 2 - 3 ger viktig information om funktionernas perioder och symmetrier.
  Dessa formler innehåller information som också finns nedlagd i funktionernas geometriska definition (m.hj.a. enhetscirkeln) eller i funktionernas grafer (se också nästa sida). Kommer man alltså ihåg hur graferna ser ut så har man nästan formlerna 2-3 till skänks.
  M.hj.a. dessa formler kan man också lösa problem där det gäller att bestämma sinus och cosinus av kända vinklar som dock ligger utanför intervallet 0 < v < .

  Ex. cos(14/3) = cos(4 + 2/3)= cos(2/3) = - cos( - 2/3) = - cos(/3) = -1/2.

  Övning 5.1 ger en del träning på sådant.

  5A.2 Trigonometriska funktioner (forts.)

  Den viktigaste geometriska representationen av de trigonometriska funktionerna är naturligtvis deras grafer.
  Som påpekades i samband med de trigonometriska formlerna 2-3 innehåller graferna en massa information som bl.a. kan formuleras som formler.

  Här nedan är graferna för sinus och cosinus.
  Lägg samtidigt märke till hur dessa kurvor skär linjer av typ y=konstant.
  Detta har nämligen betydelse i samband med trigonometriska ekvationer.

  

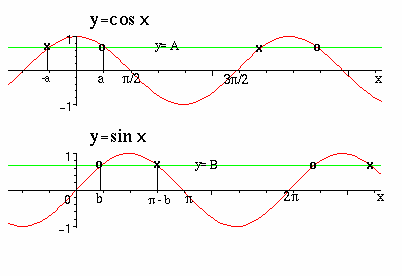
  Sinus- och cosinusfunktionerna har oändligt många nollställen. Detta är en egenskap, som exempelvis inga polynom har. Att hantera oändligt många nollställen innebär en speciell svårighet.

  Nollställena för sinusfunktionen är de tal x = n som erhålles då n antar alla heltalsvärden, dvs n = 0, ±1, ±2, ±3, osv.
  

  OBS, I fortsättningen i detta avsnitt underförstår vi att uttryck som innehåller n står för den mängd som erhålles då n antar alla heltalsvärden.

  Cosinusfunktionen har nollställena x = /2 + n

  Med stöd av graferna ovan och kommentarerna till höger kan man ställa upp följande regler för lösningar av ekvationerna:

  sin x = sin a      har lösningen:

  

  cos x = cos a      har lösningen:

  

  Trigonometriska funktioner (forts. 2)

  Här nedan följer två exempel på lösning av trigonometriska ekvationer :
  

  

  Övning 5.2 innehåller exempel på samma typer av ekvationer.

  Ytterligare exempel följer på nästa sida.

    
  Trigonometriska funktioner (forts. 3)
   I följande  exempel har man nytta av formlerna för
   dubbla vinkeln: sin 2x = ... och cos 2x = ...
   
   (se trig.formelsidan).
    
    
  Även substitutioner kan komma till användning:
   
  
   
  
   
  
   Övning5.3 innehåller likartat material.
  
   Därefter är du säkert mogen för sista testet,  Test 5.