INTRO

2C:1
2C
2C:2
Polynom-
ekvationer.

2C.1 : Kvadratkomplettering.

Man märker snart att det som är intressantast då det gäller resultatet av en kvadratkomplettering : (x-a)2 + b är tecknat på den kvarblivna konstanttermen b.

I fallet
(x-1)2 - 1 är denna term negativ, vilket bl.a medför att motsvarande andragradsekvation (x-1)2 - 1 = 0 har reella rötter.

Däremot:
(x-1)2 + 1 = 0 har inga reella rötter , vilket beror på att högerledet alltid är > 0. Man kan också utläsa av uttrycket (x-1)2 + 1 att det har minimumvärdet 1 då x = 1.

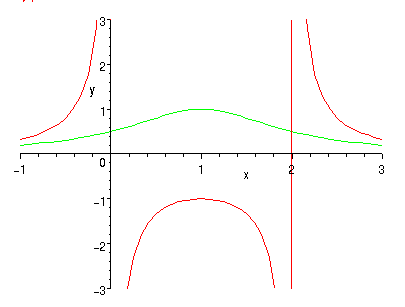
Om man sätter dessa två uttryck i nämnaren och alltså bildar funktionerna

f(x) = 1/((x-1)2 - 1) resp.

g(x) = 1/((x-1)2 + 1)

finner man en dramatisk skillnad i funktionernas grafer som beror på att nåmnaren i fallet y=f(x) har nollställen i x= 0 och 2 :

(y = f(x) : röd och y=g(x) : grön).

Länk.

Thomas Harriot
1560 - 1621 		Den engelske matematikern Thomas Harriot brukar nämnas bland dem, som tillsammans med Viète, utvecklade den algebraiska notationen, med variabler och parametrar.
Denna länk leder till hans biografi.
I slutet av den artikeln finns ett intressant exempel på hur Harriot genomförde sina beräkningar. I exemplet löser han en viss fjärdegradsekvation med hjälp av upprepade kvadratkompletteringar. Lägg märke till att han använder 'a' som variabel och skriver a4 som aaaa.
Han har ingen notation för att upphöja ett sammansatt uttryck till 2 utan går direkt från 'aa + 2a + 1' till 'a + 1 ' genom rotutdragning.