2C.1 : Kvadratkomplettering. I fallet
Däremot: Om man sätter dessa två uttryck i nämnaren och alltså bildar funktionerna f(x) = 1/((x-1)2 - 1) resp. g(x) = 1/((x-1)2 + 1) finner man en dramatisk skillnad i funktionernas grafer som beror på att nåmnaren i fallet y=f(x) har nollställen i x= 0 och 2 : 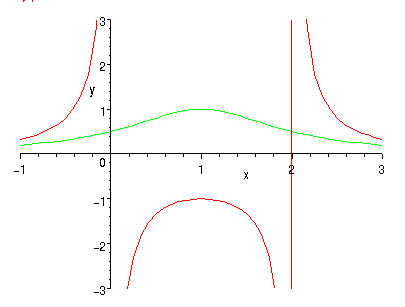
|
2C.2 : Polynomekvationer.
Här till vänster finns en länk som leder till allmänna formeln för tredjegradsekvationen
samt ett exempel på dess användning.
Ingen lyckades dock, vilket norrmannen Nils Henrik Abel (1802-1829) kunde förklara genom att bevisa den principiella omöjligheten av att uttrycka allmänna lösningarna till femtegradsekvationerna och högre medelst rötter av typ 'n:e roten ur', (samt de vanliga räknesätten +,· och /). Några länkar till detta lämnas om detta ganska dramatiska skede av matematikens historia här till höger. |
TredjegradsekvationenFörst inser man att den allmänna tredjegradsekvationen(1) az3 + bz2 + cz + d = 0
(2) x3 + px + q = 0
genom substitutionen z = x - b/(3a). Så det räcker alltså att ange lösningen till ekvation (2). Inför nu beteckningarna D = (p/3)3 + (q/2)2. (*) (**) De tre rötterna x1, x2 och x3 kan då uttryckas på följande sätt: 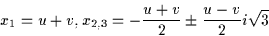
Detta visades troligen först av den italienske matematikern del Ferro (1465 - 1526).
Exempel: x3 - 6x + 4 = 0 Här är p = -6, q = 4 samt D = (-6/3)3 + (4/2)2 = -8 + 4 = -4. Uttrycken under tredjerötterna i (*) och (**) ovan kan därför skrivas -2 + 2i resp. -2 - 2i. Nu kräver lösningsformeln att man drar tredje roten ur dessa komplexa uttryck, något som 1500-talsmatematikerna hade stora problem med.
(De hade dessutom egentligen inte upptäckt de komplexa talen än och skrev inte som vi gör I detta exempel kan man dock komma vidare genom att observera att (1+i)3 = -2 +2i och (1-i)3 = -2-2i. Man får därför faktiskt: u = 1 + i och v = 1 - i , varav x1 = 2,
x2 = -1 + i2 x3 = -1 - i2 Som synes har ekvationen tre reella rötter. |
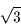 = -1 -
= -1 -