INTRO

3A:1
3A
Ex 3.1

Ex 3.2

Övn 3.1

Övn 3.2

TEST 3

3A.2 : Kvadratrötter i ekvationer 2.


Följande exempel visar två orsaker till varför man måste pröva de erhållna rötterna efter en kvadrering:

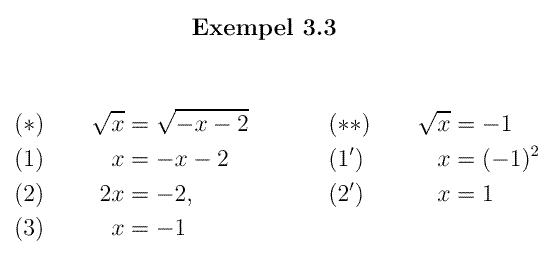
I den vänstra ekvationen (*) förändras definitionsmängderna eftersom rottecknen försvinner efter kvadreringen.
I (*) finns restriktionen att uttrycken under rottecknen inte får anta negativa värden.
I (1) finns inte någon sådan restriktion.
Men eftersom den erhållna roten x=-1 ger ett negativt värde för uttrycket under rottecknet i (*), måste denna rot slopas.


I högra ekvationen (**) uppträder samma effekt som i Ex 3.2.
Den erhållna roten x=1 ger olika värden, 1 resp. -1 i (**).
Efter kvadrering ger dock ekvationen (1') likheten
1= (-1)2.

Prövning visar alltså att de båda erhållna rötterna var falska.
Bägge ekvationerna saknar i själva verket lösning.

Kommentarer.
Att ekvation (**) saknar lösning är uppenbart eftersom ett kvadratrotsuttryck aldrig kan anta ett negativt värde som -1 i högerledet.

Att ekvation (*) saknar lösning är inte lika självklart.
Alla ekvationer av typ 'kvadratrot=kvadratrot' saknar inte lösning.
Men närmare undersökning visar att definitionsmängderna för funktionerna i vänster- och högerleden i (*) inte har något gemensamt tal. Därmed kan inte (*) ha någon lösning.
(VL är definierat för x>0 och x=0, medan HL är definierat för x<-2 och x=-2.)