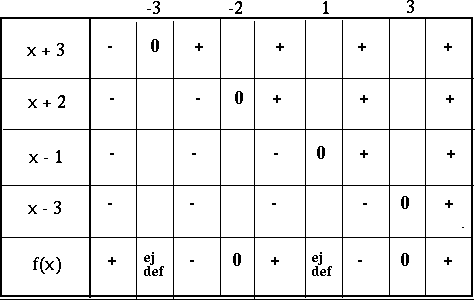
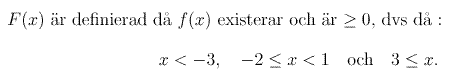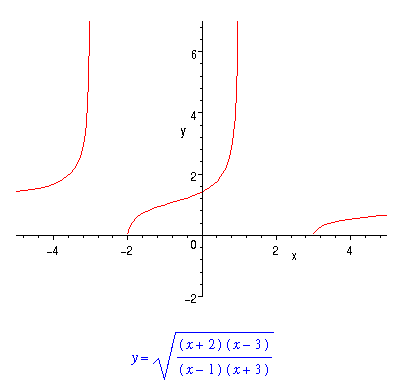3A.1 : Kvadratrötter och deras definitionsmängder.

Det finns en elementär metod att avgöra teckenväxlingen för rationella funktioner.
Metoden bygger på att funktionen faktoriseras och att undersökningen utföres för varje faktor för sig varefter resultaten sammanställs i en teckentabell:

Övning 3.1 handlar om sådana problem som kan lösas med teckentabeller av ovanstående typ.

3A.2 : Kvadratrötter i ekvationer 1.

Vid lösning av ekvationer som innehåller rotuttryck måste man normalt kvadrera bägge led för att komma vidare.
Detta kan leda till att nya rötter tillkommer i ekvationen vilket gör att man alltid måste pröva de erhållna rötterna i ursprungsekvationen.

I Ex 3.3 behandlas mer i detalj vad som kan hända vid kvadrering i en ekvation med rotuttryck.

3A.2 : Kvadratrötter i ekvationer 2.

Följande exempel visar två orsaker till varför man måste pröva de erhållna rötterna efter en kvadrering:

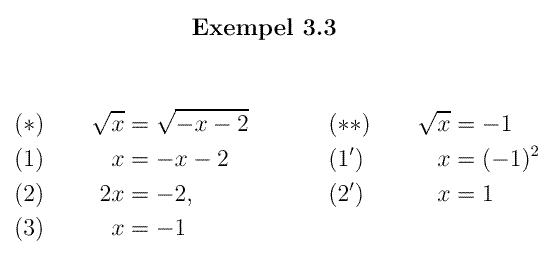
I den vänstra ekvationen (*) förändras definitionsmängderna eftersom rottecknen försvinner efter kvadreringen.
I (*) finns restriktionen att uttrycken under rottecknen inte får anta negativa värden.
I (1) finns inte någon sådan restriktion.
Men eftersom den erhållna roten x=-1 ger ett negativt värde för uttrycket under rottecknet i (*), måste denna rot slopas.


I högra ekvationen (**) uppträder samma effekt som i Ex 3.2.
Den erhållna roten x=1 ger olika värden, 1 resp. -1 i (**).
Efter kvadrering ger dock ekvationen (1') likheten
1= (-1)2.

Prövning visar alltså att de båda erhållna rötterna var falska.
Bägge ekvationerna saknar i själva verket lösning.