| INTRO |
1B:1
 1B
1B
Ex 1.1(A)
1B : Fullständig undersökning av ekvationerna.
Vid lösningen av parameterekvationerna i 1A visade det sig att de erhållna lösningarna inte gällde för alla värden på de ingående parametrarna.
Lösningen till ekvationen i Ex 1.1 hade uttrycket a - b i nämnaren
vilket betyder att denna lösning inte kan gälla då a = b.
Denna ekvation borde därför ha undersökts speciellt för bl.a. detta fall.
I Ex 1.2 förekommer
uttrycket x-a i ekvationens ena nämnare.
Därmed kan inte lösningen x= (a+1)/2 gälla för det a-värde
som ger x-a = 0 .
Detta a-värde fås av 0 = x-a = (a+1)/2 - a = 1/2 -a/2 = 0 dvs. a = 1.
Även ett annat a-värde visar sig vara speciellt i
detta fall.
En fullständig utredning av Ex 1.2 och 1.1 ger vi som övningar 1B.1(a) och (b).
Vi börjar med att undersöka en enklare ekvation:

De speciella a-värdena undersöks därefter:
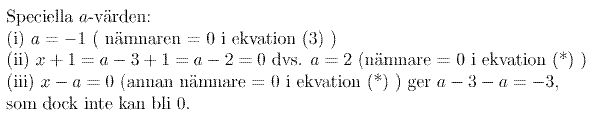
Insättning av de speciella a-värdena i (*) :

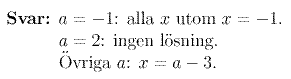
Kommentarer.
De speciella parametervärdena, som måste undersökas särskilt,
bestäms alltså på följande sätt :
Undersök varje nämnare som förekommer i ekvationen, i svaret eller någonstans i uträkningarna.
Bestäm de parametervärden som ger nämnaren värdet 0.
Om nämnaren innehåller en variabel x måste man ersätta
x med
den generella lösningsformeln
för att se vilka parametervärden som ger nämnaren 0-värdet.
(Detta görs i fallen (ii) och (iii) här till vänster.)
Sätt till slut in alla sådana speciella parametervärden i ekvationen och lös ekvationen för dessa fall.
Samma procedur gäller också då det finns flera parametrar.
Varför är inte x=-1 en lösning då a=-1 ?
Jo, för x=-1 är nämnarna = 0 och därmed är inte ekvationens led definierade för detta x-värde.