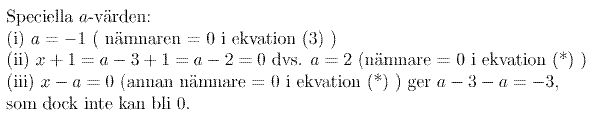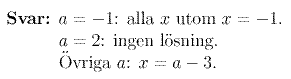1B : Fullständig undersökning av ekvationerna.

Vid lösningen av parameterekvationerna i 1A visade det sig att
de erhållna lösningarna inte gällde för alla värden på de ing&ar
ing;ende parametrarna.

Lösningen till ekvationen i Ex 1.1 hade uttrycket a - b i
nämnaren vilket betyder att denna lösning inte kan gälla då
a = b.
Denna ekvation borde därför ha undersökts speciellt bl.a. detta fall.

I Ex 1.2 förekommer uttrycket x-a i ekvationens ena nämnare.
Därmed kan inte lösningen x= (a+1)/2 gälla för
det a-värde som ger x-a = 0 .
Detta a-värde fås av 0 = x-a = (a+1)/2 - a = 1/2 -a/2 = 0 dvs. a = 1.
Även ett annat a-värde visar sig vara speciellt i detta fall.

En fullständig utredning av Ex 1.2 och 1.1 ger vi som övningar 1B.1(a) och (b).

Vi börjar med att undersöka en enklare ekvation:

De speciella a-värdena undersöks därefter:

Insättning av de speciella a-värdena i (*) :