Ekvationer med prövning.

Vissa ekvationer fordrar en sådan behandling vid lösandet att det kan slinka falska rötter.
Ekvationslösning består ju oftast av en följd av ekvationer där de senare utgör omformningar av de tidigare.
En falsk rot är en lösning till de senare versionerna av ekvationen som dock inte är en lösning till den ursprungliga ekvationen.

En falsk rot måste naturligtvis förkastas.
Medlet mot falska rötter är prövning i ursprungsekvationen.
Det är dessutom bra om man lär sig förstå när prövning behövs. All ekvationslösning fordrar nämligen inte prövning.

De vanligaste fallen då prövning behövs uppträder i samband med kvadratrötter och logaritmer.

Då ekvationer innehåller kvadratrötter måste man oftast kvadrera bägge leden av ekvationen för att bli av med dem.
Ibland måste man kvadrera flera gånger för att bli av med alla kvadratrötter.

Det finns två anledningar till att man måste pröva rötterna efter att man har kvadrerat bägge led.

1. Dels kan nya rötter ha tillkommit eftersom existensområdet för ekvationens funktioner utökades när kvadratrötterna eliminerades.

2. Dels kan nya rötter ha tillkommit genom själva kvadreringseffekten: 3 är ju inte = -3, men efter kvadrering blir talen lika: 3² = (-3)² = 9.

Exempel 2 ger två enkla. typiska exempel på dessa effekter.

I samband med logaritmer uppstår ofta fall 1 ovan, utökning av existensområdet, när man går från en ekvation av typen ln A = ln B till A = B.

Grafer

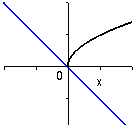
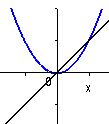
y = -x , y = sqrt(x)	y = x2 , y = x	De två graferna avses visa kvadreringseffekten vid ekvationslösning. Till vänster ses de båda leden i ekvationen -x = sqrt(x) (sqrt(x) = 'roten ur x' ) framställda med varsin graf. Skärningspunktens x-koordinat ( här x=0 ) är ekvationens lösning. Till höger syns den kvadrerade ekvationen framställd på samma sätt. Man ser att den nya roten x=1 har tillkommit p.g.a kvadreringen Före kvadreringen hade man -1 i vänsterledet och +1 i högerledet.
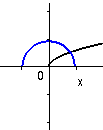y=sqrt(6-x2) , y = sqrt(x).	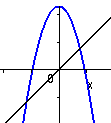y = 6-x2 , y = x.	Dessa grafer visar effekten av utökat existensområde efter kvadrering. Ekvationen är sqrt(6-x2) = sqrt(x). där vänsterledets funktion existerar i och mellan punkterna -sqrt(6) och +sqrt(6), medan högerledets rot existerar då x>=0. Det finns en skärningspunkt, dvs rot, för x=2. Efter kvadreringen försvinner alla restriktioner för existensområdena och man ser att en ny falsk har tillkommit genom den nya skärningspunkten i x = -3.