Fast information sharing in proximity-based multichannel wireless networks
Introduction
This work considers the problem of distributed neighbor discovery in multi-channel wireless networks. We propose a protocol in which nodes randomly select a channel and decide whether to transmit or listen for neighbor discovery beacons. When nodes transmit, they use epidemic information dissemination to spread knowledge about all the nodes they have discovered so far.
Preliminaries
Coupon Collector: In (Vasudevan et al., 2009) the authors noted that the discovery process resembles the classical coupon collector problem in statistics.
Consider a clique network with 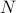 nodes, where any node can
directly communicate with any other node. Under Slotted-Aloha, the probability that a node successfully
transmits
nodes, where any node can
directly communicate with any other node. Under Slotted-Aloha, the probability that a node successfully
transmits 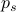 in any time slot is given by the probability a node transmits
in any time slot is given by the probability a node transmits 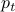 , given that
the remaining
, given that
the remaining 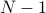 nodes remain silent. This probability (
nodes remain silent. This probability (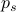 ) is given by:
) is given by:
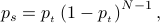
the optimal transmit probability is proven to be
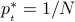 and substituting
and substituting 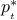 , we obtain
, we obtain 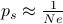 .
The classical coupon collector analysis can be formulated as follows:
.
The classical coupon collector analysis can be formulated as follows:
Let 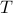 denote the number time-slots to discover all
denote the number time-slots to discover all 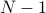 neighbors.
Let
neighbors.
Let 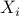 denote the time a node discovers the
denote the time a node discovers the 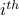 node.
Let
node.
Let 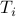 be a random variable that denotes the number of elapsed time-slots starting from the discovery of the
be a random variable that denotes the number of elapsed time-slots starting from the discovery of the 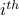 node till the discovery of the
node till the discovery of the 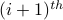 new node,
i.e,
new node,
i.e, 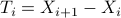 .
After the discovery of the
.
After the discovery of the 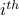 node, at any random trial, there still exists
node, at any random trial, there still exists 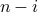 nodes to be discovered, each with probability
nodes to be discovered, each with probability 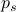 .
We can deduce that
.
We can deduce that 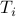 has a geometric distribution with expectation
has a geometric distribution with expectation ![E[T_i]=frac{1}{(n-i)p_s}](eqs/1030192666602906367-130.png) , and by the linearity of the expectations
, and by the linearity of the expectations ![E[T]=sum_{i=0}^{N-1}E[T_i]](eqs/8038512124521558952-130.png) .
Therefore, the expected time can be computed as:
.
Therefore, the expected time can be computed as:
![E[T]=sum_{i=0}^{N-1}E[T_i] =sum_{i=0}^{N-1}frac{1}{(n-i)p_s} approx NeH_N =Ne big( ln N+Theta(1) big) ,](eqs/5630215562779906037-130.png)
where 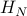 denotes the
denotes the 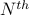 harmonic number.
harmonic number.
Multichannel coupon collector:
In multichannel coupon collector, there are (k) channels, which are
used to broadcast information. Before transmitting a packet, each node selects the
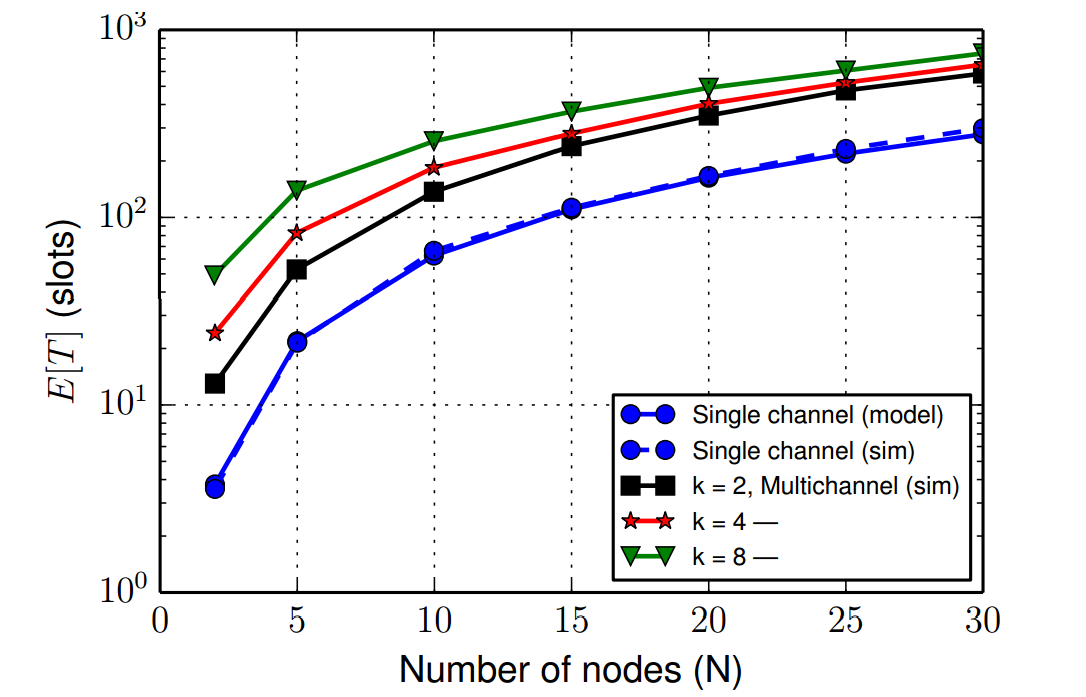
transmission channel with equal probability. Assuming there are k channels and 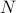 nodes, the transmission probability is given by
nodes, the transmission probability is given by 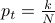 .
.
 |
|
Implications to low-power wireless communications
For low-power wireless the goal is to having a fast and energy-efficient information
exchange, which translates into having a smaller value of ![E[T]](eqs/8482911174020949727-130.png) .
.
Single channel neighbor discovery suffers many drawbacks: (i) inability to manage the radio interference properly, (ii) network performance degrades with the increase in the number of nodes, (iii) the idle probability tends to be high, which results in unnecessary long discovery times. The probability of an idle slot
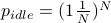 , which approaches
, which approaches 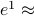 36.8% as N grows large. When the broadcast is
unreliable, i.e., when only a subset of the nodes are able to successfully decode a beacon, the discovery times will be even larger.
36.8% as N grows large. When the broadcast is
unreliable, i.e., when only a subset of the nodes are able to successfully decode a beacon, the discovery times will be even larger.
Multichannel communications alone do not do better either. For example, consider the following facts: (i) the choice of using an empirical number of channels performs worst than a single channel approach; (ii) multichannel communications alone cannot reduce the average discovery latency for any node to discovery all its neighbors.
The critical factors for enhancing neighbor discovery performance are (i) epidemic discovery, and (ii) tuning the number of channels k depending on the network size N. This is the approach we explore in this project.
Assessing the potential of multi-channel epidemic discovery
We analyze a theoretical three-phase protocol and show that it allows for a discovery-time speedup on the order of 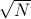 We then introduce and analyze a simpler and more easily implementable protocol
that retains many of the advantages of the theoretical protocol.
The theoretical protocol proceeds in three phases:
We then introduce and analyze a simpler and more easily implementable protocol
that retains many of the advantages of the theoretical protocol.
The theoretical protocol proceeds in three phases:
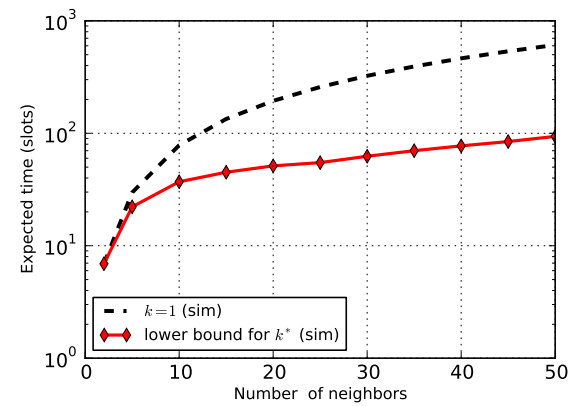 |
Single channel vs multichannel epidemic discovery with k channels; given
the network size N we choose k (lower bound on |
Multichannel coupon collector: in the first phase, we run k parallel neighbor discovery processes (one per channel), each with N/k nodes (note that if N/k is not an integer we take integers close to N/k, so that the number of nodes in all channels is N);
Epidemic coupoun collector: in the second phase, one node from each of the k channels enters an epidemic dissemination process where nodes broadcast information about all nodes discovered in their respective channels;
finally, the k nodes return to their original channels and broadcast information about all nodes in the network.
The equation gives the sum of ![E[T]](eqs/8482911174020949727-130.png) for the coupon collector analysis of the
three phase algorithm.
for the coupon collector analysis of the
three phase algorithm.
![E[T] = frac{N}{k}left[lnleft(frac{N}{k} right) +Theta(1)right] + kbig(ln k + Theta(1)big)+ Theta(1) approx frac{N}{k}ln(frac{N}{k})+kln k](eqs/4485449400783615567-130.png)
Admittedly, this protocol have the first and second phases asymptomatic termination.
However, it allows for a simple discovery time estimate (see Figure). Given the
network size N we choose 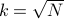 (lower bound on
(lower bound on 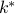 ) that minimizes
) that minimizes ![E[T]](eqs/8482911174020949727-130.png) , which gives
, which gives
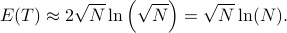
Hence, the protocol achieves a speedup of roughly 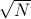 compared to the singlechannel protocol
compared to the singlechannel protocol
References
Vasudevan et al., 2009, “Neighbor discovery in wireless networks and the coupon collector’s problem”, ACM Mobicom’09