Deterministic information-exchange with epidemics in multihop wireless networks
Introduction
Deterministic neighbor discovery protocols on the other hand, schedule listening and transmission phases to offer a deterministic guarantee on the worst-case neighbor discovery time.
In this work, we therefore propose protocol enhancements that allow for faster average discovery times while maintaining the same worst-case guarantees. Specifically, we propose an epidemic information dissemination mechanism to speed up the discovery times in deterministic neighbor discovery protocols. The main idea is to let each node broadcast information about the beaconing slot locations of already discovered neighbors, so that other nodes in the network that are neighbors to these nodes can discover them much earlier. This simple extension to classical neighbor discovery protocols has two key advantages which lead to strong performance improvements while still ensuring determinism in the discovery.
Preliminaries
Our protocol is an asynchronous cyclic slot-based deterministic discovery protocol based on the ideas developed by previous protocols of this type
(emph{e.g.}, Searchlight, Hello}).
These protocols operate in cycles defined by two parameters: (a) the period of 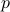 slots and (b) the hyper-period
slots and (b) the hyper-period 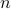 specifying the number of
periods within a cycle. Slot sizes are fixed and equal for all nodes. To save energy, nodes are not active throughout, but wake up and communicate occasionally.
A discovery occurs when the active slots of two nodes overlap. Active slots are classified into two categories: (i) anchor slots, which always occupy the first position within a period, and
(ii) probe slots, whose positions within the cycle vary with time.
specifying the number of
periods within a cycle. Slot sizes are fixed and equal for all nodes. To save energy, nodes are not active throughout, but wake up and communicate occasionally.
A discovery occurs when the active slots of two nodes overlap. Active slots are classified into two categories: (i) anchor slots, which always occupy the first position within a period, and
(ii) probe slots, whose positions within the cycle vary with time.
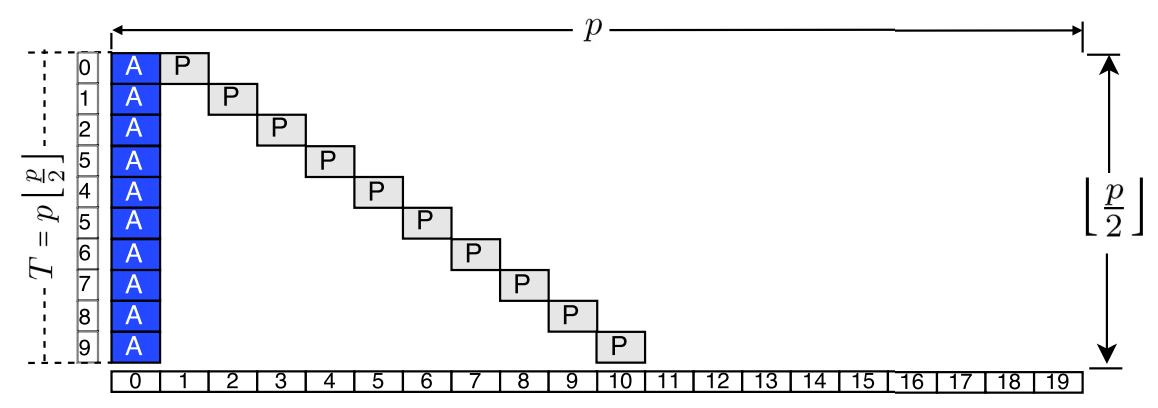
Searchlight is based on the observation that the temporal distance between the anchor slots of any two nodes is constant and upper bounded by
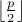 .
Hence, by adding an additional probing action that searches slots
.
Hence, by adding an additional probing action that searches slots 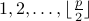 ,
discovery is guaranteed. Specifically, Searchlight increments the probe slot position by one every hyper-period, and resets the position to
,
discovery is guaranteed. Specifically, Searchlight increments the probe slot position by one every hyper-period, and resets the position to
 when it exceeds
when it exceeds 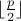 . In this way, Searchlight uses
. In this way, Searchlight uses 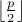 hyper-periods and the total number of slots
required for discovery is never more than
hyper-periods and the total number of slots
required for discovery is never more than 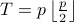 .
.
 |
In deterministic neighbor discovery protocols, the positions of the active slots (both anchor and probe slots) for each node are pre-determined. This means that once the period and the position of an anchor are known, one is able to determine where the future anchor slots will appear. Based on this observation, we propose a protocol that lets nodes convey information about already discovered neighbors in their beacons. This allows for nodes that receive a discovery beacon to compute the anchor location of nodes that it has not yet detected itself, and target its probing actions to these slots. The use of epidemic information allows to maintain similar worst-case characteristics to other deterministic neighbor discovery protocols, but improves the practical pairwise neighbor discovery times and the average neighbor discovery termination times (when all nodes have discovered all their neighbors). |
Protocol schedule design
Epidemic probing, activates extra probe slots to rapidly discover possible neighbors within a hyper period.
Epidemic probing mechanism
Each node 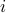 maintains, among others, data about its one-hop neighbors. We will demonstrate how this data can be spread epidemically and how nodes can use it to target discovery probes to speed up the neighbor discovery process.
maintains, among others, data about its one-hop neighbors. We will demonstrate how this data can be spread epidemically and how nodes can use it to target discovery probes to speed up the neighbor discovery process.
Consider a node 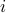 and let
and let 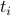 denote the number of time slots since the node was booted. Then
denote the number of time slots since the node was booted. Then
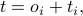
where 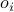 is an unknown offset between the global and local notions of time. The local timer
is an unknown offset between the global and local notions of time. The local timer 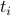 can be also expressed in terms of its period
can be also expressed in terms of its period 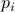 and its offset
and its offset 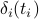 from the anchor slot of the emph{current period} (emph{i.e.}, the period that slot
from the anchor slot of the emph{current period} (emph{i.e.}, the period that slot 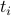 belongs to):
belongs to):
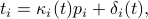
where 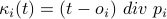 is the number of periods that have passed since boot time of node
is the number of periods that have passed since boot time of node 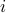 , and
, and
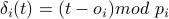 is the number of time slots since the most recent period start.
Although nodes do not have access to the global time
is the number of time slots since the most recent period start.
Although nodes do not have access to the global time 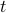 , they always know the corresponding values of
, they always know the corresponding values of 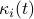 and
and 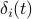 .
.
Let 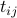 be the time (or the slot, since we assume that the slots of all nodes are aligned) emph{of the global clock} at
which node
be the time (or the slot, since we assume that the slots of all nodes are aligned) emph{of the global clock} at
which node 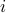 discovers node
discovers node 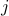 . Since we assume mutual discovery,
. Since we assume mutual discovery, 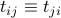 . When node
. When node 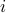 discovers node
discovers node 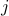 , it shares
(i) the number of slots
, it shares
(i) the number of slots 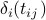 of the current slot from the anchor slot of the current period and the size of its period
of the current slot from the anchor slot of the current period and the size of its period 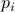 .
Node
.
Node 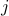 shares the corresponding information with node
shares the corresponding information with node 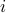 . Thus, node
. Thus, node 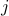 can deduce that future anchor slots of node
can deduce that future anchor slots of node 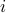 will appear at
will appear at
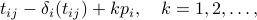
and, similarly, node 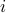 can deduce that future anchors of node
can deduce that future anchors of node 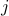 will appear at slots
will appear at slots
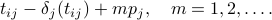
As a result, given the offset and the period, each of the nodes can determine when anchor slots of the other node will appear.
For example, node 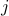 can compute the offset of the anchor slots of node
can compute the offset of the anchor slots of node 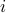 emph{relative to its own anchor slots} as the
difference between the future anchor slots for both nodes, i.e., by subtracting the first two equations to find
emph{relative to its own anchor slots} as the
difference between the future anchor slots for both nodes, i.e., by subtracting the first two equations to find
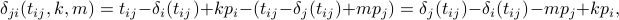
where 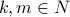 (
(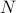 is the set of natural numbers). This will be the key expression for computing and updating
is the set of natural numbers). This will be the key expression for computing and updating 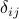 ,
the offset to the first anchor slot of node
,
the offset to the first anchor slot of node 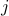 relative to the start of the most recent period of node
relative to the start of the most recent period of node 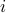 . Note that no reference to global
time is needed to evaluate the expression, all that is required is the quantity
. Note that no reference to global
time is needed to evaluate the expression, all that is required is the quantity 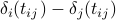 and the period size of the nodes.
and the period size of the nodes.
By increasing 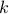 and
and 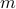 node
node 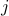 finds the number of slots between the
finds the number of slots between the 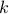 -th anchor slot (after the discovery time) of node
-th anchor slot (after the discovery time) of node 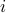 and the
and the
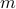 -th anchor slot of node
-th anchor slot of node 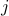 . As a result, at every time instant
. As a result, at every time instant 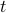 , node
, node 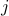 is able to determine
is able to determine 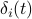 of every node
of every node 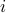 discovered so far.
discovered so far.
In our protocol, node 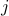 computes the offset
computes the offset 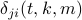 at every anchor slot. Even though it is not necessary, for simplicity of
exposition we assume that the offsets are updated also at the probe slots where there can be a new discovery and a node has to share information
with other nodes. In this case, at a discovery time
at every anchor slot. Even though it is not necessary, for simplicity of
exposition we assume that the offsets are updated also at the probe slots where there can be a new discovery and a node has to share information
with other nodes. In this case, at a discovery time 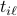 , node
, node 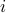 can provide the triplet
can provide the triplet 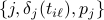 about already
discovered node
about already
discovered node 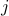 to any newly discovered node
to any newly discovered node 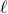 . Then, node
. Then, node 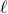 follows the same procedure for computing the relative offset
follows the same procedure for computing the relative offset 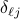 as in equation above.
as in equation above.
Targeted probes for direct discovery
When nodes 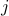 and
and 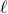 discover each other, node
discover each other, node 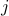 provides, apart from its information (
provides, apart from its information (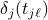 and
and 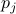 ), the corresponding information for
all nodes
), the corresponding information for
all nodes 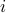 discovered by
discovered by 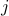 until time instant
until time instant 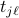 . As a result, node
. As a result, node 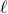 can determine the location of the anchor slots of node
can determine the location of the anchor slots of node 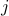 (for passing
this information to future discoveries) and those of its discovered neighbors, for which it will initiate targeted probes for direct discovery.
(for passing
this information to future discoveries) and those of its discovered neighbors, for which it will initiate targeted probes for direct discovery.
At discovery of node 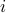 by node
by node 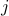 ,
, 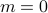 and node
and node 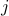 computes
computes 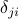 by adjusting
by adjusting 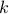 until it finds the smallest non-negative value of
until it finds the smallest non-negative value of
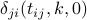 ; if we denote the corresponding
; if we denote the corresponding 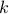 by
by 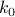 , we have
, we have 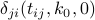 . At the next period start of node
. At the next period start of node 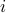 ,
, 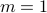 so
so
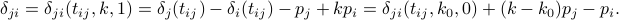
To maintain its data structure up to date, node 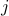 now needs to adjust
now needs to adjust 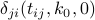 so that it becomes equal to the smallest
non-negative value of
so that it becomes equal to the smallest
non-negative value of 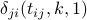 . We see from the expression above that we can do this by subtracting
. We see from the expression above that we can do this by subtracting 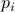 from the current value
of
from the current value
of 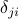 , and then add multiples of
, and then add multiples of 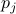 until the value becomes non-negative.
until the value becomes non-negative.
Duty-cycle
In deterministic neighbor discovery for which every period 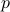 has an anchor, the duty cycle
has an anchor, the duty cycle 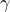 is given by
is given by
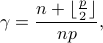
where 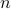 is the number of periods in a hyper-period. Without receiving any epidemic information, the duty-cycle is the same as the deterministic neighbor discovery
protocol used as the basis of our algorithm; in this case it is Searchlight. If there is activation of extra probe slots due to epidemic discovery, our protocol uses extra slots.
Therefore, the instantaneous duty-cycle in period
is the number of periods in a hyper-period. Without receiving any epidemic information, the duty-cycle is the same as the deterministic neighbor discovery
protocol used as the basis of our algorithm; in this case it is Searchlight. If there is activation of extra probe slots due to epidemic discovery, our protocol uses extra slots.
Therefore, the instantaneous duty-cycle in period 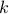 is given by
is given by
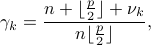
where  is the total number of extra slots activated during period
is the total number of extra slots activated during period  . When we use Searchlight and striped transmission, the instantaneous duty-cycle becomes
. When we use Searchlight and striped transmission, the instantaneous duty-cycle becomes
As  increases and almost all neighbors have been discovered,
increases and almost all neighbors have been discovered, 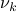 goes to zero and the instantaneous duty-cycle is the same as that of Searchlight.
The average duty cycle over
goes to zero and the instantaneous duty-cycle is the same as that of Searchlight.
The average duty cycle over 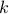 periods is given by
periods is given by
The average duty cycle as 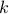 goes to infinity is given by
goes to infinity is given by
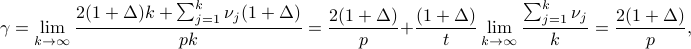
which is the same as that of Searchlight.
Performance evaluation
We study the following key metrics: (i) discovery latency, i.e., the longest time recorded for any node in the network to discover all its neighbors; (ii) energy consumption, quantified by the duty cycle during the discovery process; and (iii) the performance in dynamic scenarios, where two networks merge, or a single node joins an already converged network.
Worst-case latency
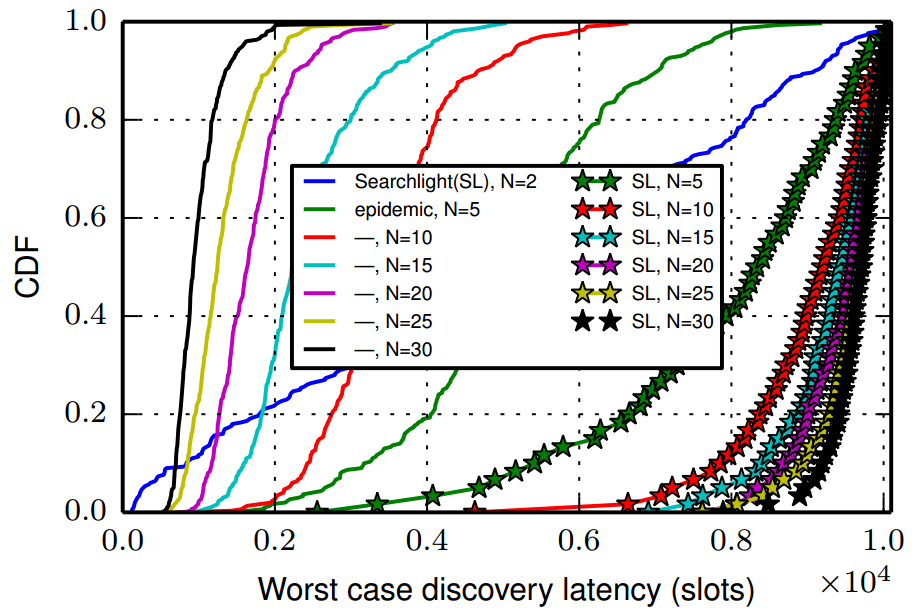 |
The Figure compares the discovery latency of Searchlight with its epidemic counterpart for clique networks networks with different number of nodes. |
The figure is based
on 1000 network realizations (that is, 1000 different realizations
of the period offsets for the nodes), each of which
is simulated for 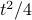 time slots. We have used p = 200,
which corresponds to a duty cycle of 1% and a worst-case
discovery time for Searchlightof 10000 slots.
time slots. We have used p = 200,
which corresponds to a duty cycle of 1% and a worst-case
discovery time for Searchlightof 10000 slots.
Observation: When there are only two nodes in the network, Searchlightand our epidemic discovery protocol are equivalent. However, as the number of nodes increase, the likelihood that two nodes have an unfortunate offset increases, and many node pairs experience a latency close to the worst-case bound. With epidemic probing, on the other hand, the performance improves as the network size increases. This result can be explained from the fact the larger the clique size, the more information tends to be conveyed by the epidemic probing, and the faster the discovery process comes to an end.
Energy consumption
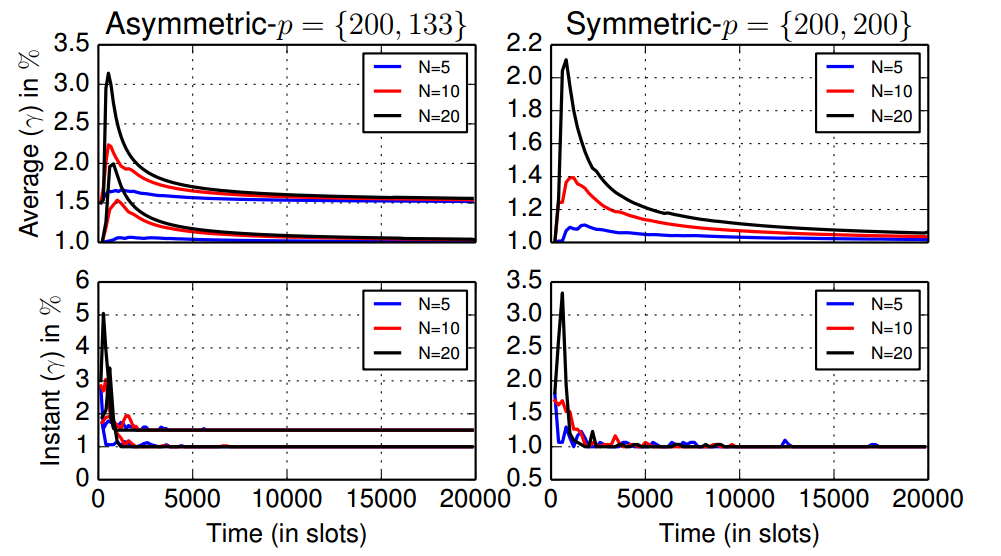 |
The behavior is similar for asymmetric periods |
Observation: Average energy consumption over time (top) and instant energy consumption (bottom) for asymmetric (left) and symmetric (right) discovery. There is an initial increase in the energy consumption, due to the discovery process, but after a while the average energy returns to its nominal value.
Dynamic scenarios
The dynamic increase in duty cycles “when needed” is particularly useful in dynamic scenarios. To make the point, we first consider a scenario where two fully converged networks merge. On such scenario could be when two buses drop their passengers, whose devices have discovered each other during the bus ride, simultaneously at a bus station. The epidemic probing then allows to bootstrap the discovery process at the bus station and allows a rapid and energy efficient discovery of the complete network.
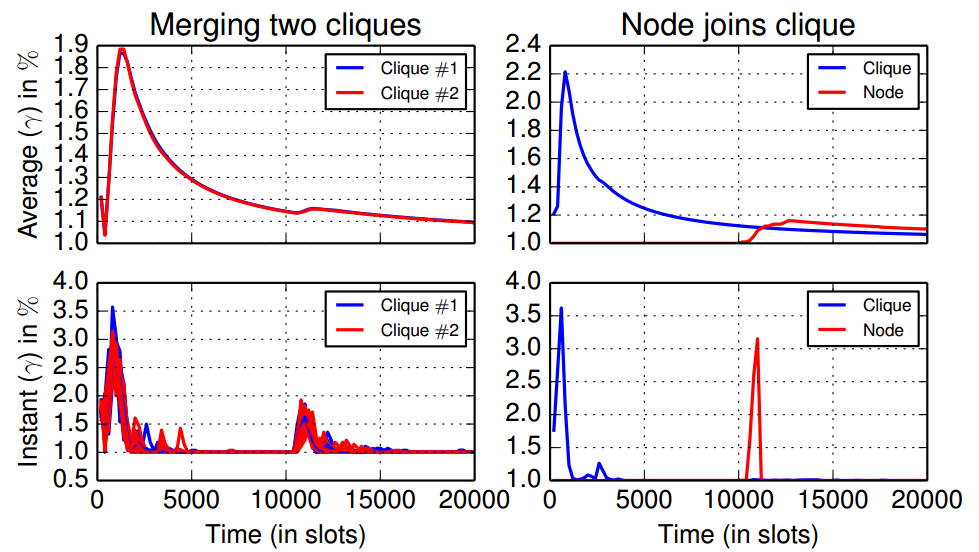 |
Merging two clique networks (left) and a node joins a fully
converged clique network (right). At |
Observation: The initial network discovery on each bus is similar to previous simulations. However, when the two nodes merge, the discovery of the full network is both faster and much more energy efficient. This performance improvement is because when the networks merge, the nodes convey a lot of epidemic information already from the start.
We show the energy consumption when a single node joins a converged network. This node can discover all its neighbors quickly and a modest and temporary increase of duty cycle. The impact on the energy consumption of the other network node is very limited.
Extension to multihop networks
In practice, the network topology is often more complicated than a single clique, and packet transmissions are unreliable. This section extends the concepts developed in the previous sections to neighbor discovery in general networks.
 |
An example of a random network topology with |
When the network is subject
to losses (due to fading or collisions), we cannot just probe
once, but should allow for a few discovery attempts. This
leads us to include a retry limit  on the number of times
we attempt to probe a node after it has become known to
us. The selection of
on the number of times
we attempt to probe a node after it has become known to
us. The selection of  involves a trade-off between energy
expenditure for targeted probing of nodes that are not
neighbors and the the probability of failing to detect direct
neighbors.
involves a trade-off between energy
expenditure for targeted probing of nodes that are not
neighbors and the the probability of failing to detect direct
neighbors.
Energy consumption
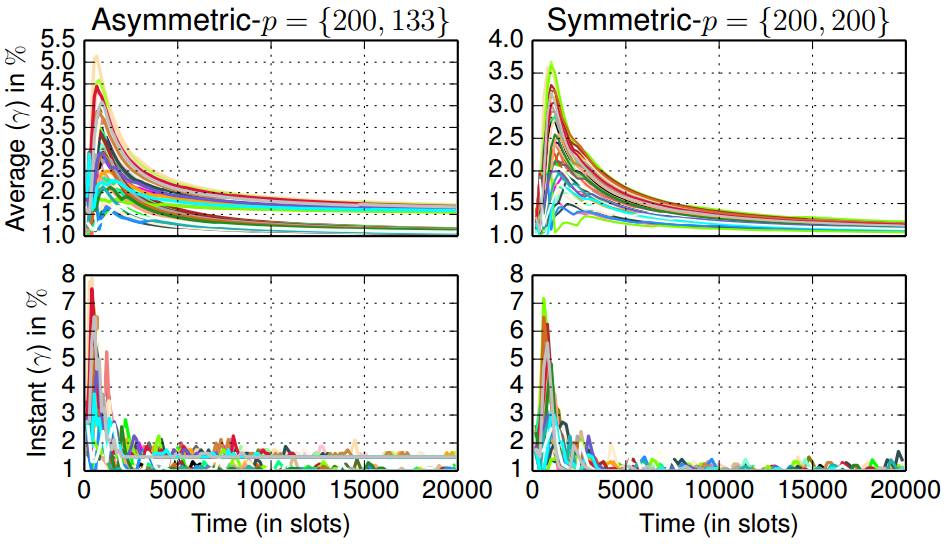 |
Average (top) and instantaneous (bottom) energy (duty-cycle) over time in a multihop network using asymmetric (left, p = f200; 133g) and symmetric (right, p = f200; 200g) discovery. Nodes with many neighbors will experience a high duty-cycle at the beginning due to epidemics since it will activate many extra slots to discover its neighbors. |
Experimental validation: Indriya testbed
We conducted all our experiments at the Indriya testbed. Indriya is a large-scale and low-power wireless sensor network testbed, consisting of 100 TelosB motes built on an active-USB infrastructure at National University of Singapore.
Average node degree
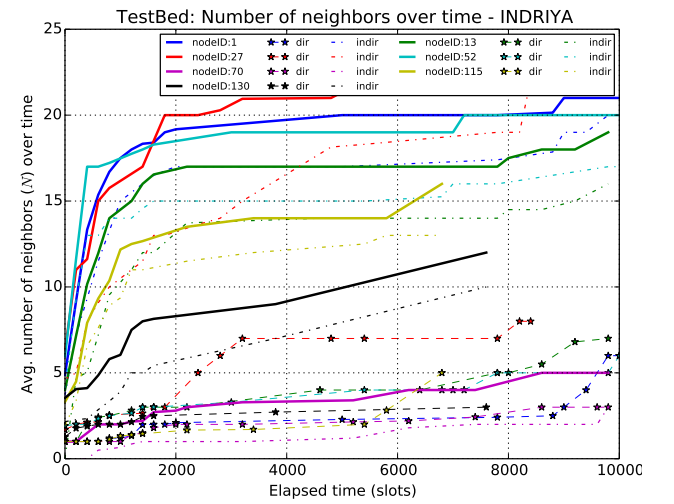 |
Average number of neighbor nodes discovered using epidemic discovery. The use of epidemics boosts considerable the total number of neighbors discovered. The solid-thick line is the total number of neighbors discovered, that is the sum of the direct discovery (dot-star ) and the indirect discoveries (dotted). |
Instant and average duty-cycle
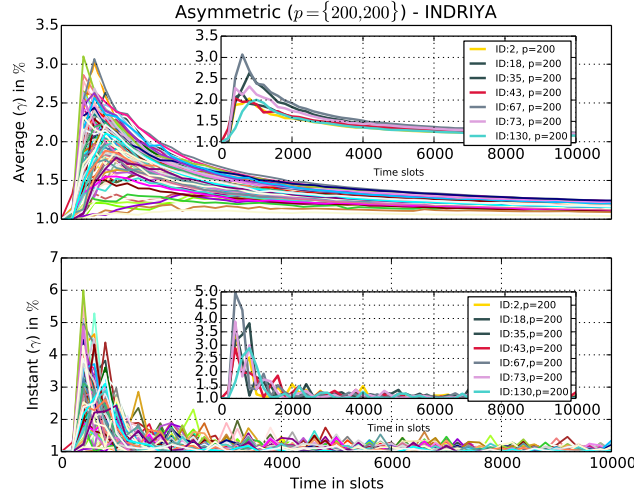 |
The Figure shows how the instantaneous duty-cycle increases momentarily, and then returns to the nominal 1%-duty cycle of Searchlight, much like what we observed in simulations. |
Observation: The small peaks observed during the stationary period are due to discovery attempts of nodes not previously known. This is also an artefact of lossy communication: sometimes, the epidemic dissemination is delayed due to packet losses. The inner plot highlights the location-dependent performance, where nodes with large two-hop neighborhoods have high peak duty cycles, while sparsely connected nodes have lower energy consumption.
Conclusions
We have proposed a simple yet novel protocol for rapid and deterministic neighbor discovery that employs epidemic probing, a mechanism that dynamically increases the number of active slots whenever this is likely to be useful. During network formation or topology changes, the protocol temporarily spends more energy in speeding up discovery and then returns to a low-energy mode. This results in a protocol with dramatically decreased discovery times and a long-term average energy consumption close to the current state-of-the-art Searchlight protocol. Significant performance benefits were reported in simulations and realworld deployments, in cliques and multi-hop networks, and under reliable and unreliable communication.
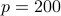 and
and
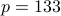 , corresponding to duty cycles of 1% and 1.5%,
respectively.
, corresponding to duty cycles of 1% and 1.5%,
respectively.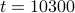 we merge both cliques,
and the results show that there is a small increase on the average dutycycle,
while the instant duty-cycle grows slightly. When a node joins a
network and due to epidemics, it quickly gathers network information,
and the results indicate that it reflects on its instant energy consumption.
we merge both cliques,
and the results show that there is a small increase on the average dutycycle,
while the instant duty-cycle grows slightly. When a node joins a
network and due to epidemics, it quickly gathers network information,
and the results indicate that it reflects on its instant energy consumption. nodes.
nodes.