I am a researcher in machine learning and geometry. I am currently focused on the robustness of neural networks and related cybersecurity issues.

Current affiliation: Technical University of Denmark
Contact: daek 'AT' kth.se

Some ongoing projects

1. Sampling algebraic varieties

In this project we develop new efficient methods for sampling algebraic data manifolds. As input we expect a system of polynomial equations defining the manifold. The output is a sample with a guaranteed density. This problem is important in geometric data analysis as a sample can be used to compute geometric features of the manifold (such as its homology groups). Closely related is the concept of reach, which is a regularity measure used throughout manifold learning. The method is based on homotopy continuation techniques for solving systems of polynomials coupled with a careful analysis of the density of the sample. This is a collaboration with S. Di Rocco (KTH) and O. Gäfvert (KTH).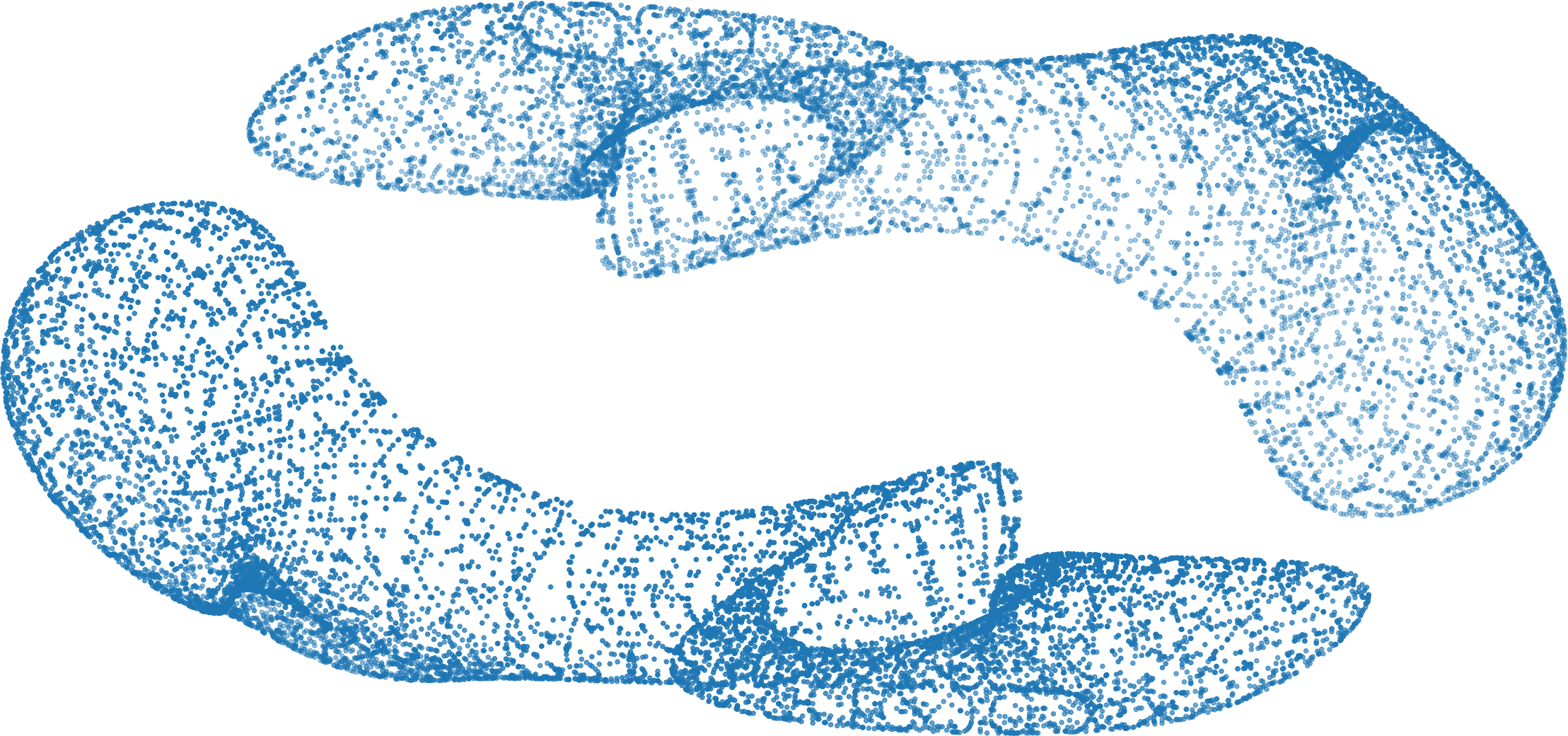

2. The Finsler geometry of generative models

In this project we explore extensions of Riemannian geometry applied to machine learning models. Riemannian geometry is by now an established tool in the machine learning community used for example to measure distance between data points and interpolation tasks. In the case of probabilistic generative models however, natural distance measures are random variables. Given a curve in the latent space a probabilistic generative model gives rise to a stochastic curve in data space. In this project we study the expected length of such curves. This induces a metric on the latent space by letting the distance between points be the infimum of the expected length over all curves joining the points. The issue with such distance measures is that they do not come from an underlying Riemannian metric. We show how such distance measures still fit into the wider framework of Finsler geometry. Finsler geometry is a little known extension of Riemannian geometry which still allows for the introduction of distances, the computation of interpolating curves etc. The project aims at introducing these mathematical ideas to the machine learning community and show how they are useful. This is a collaboration with S. Hauberg (DTU) and A. Pouplin (DTU).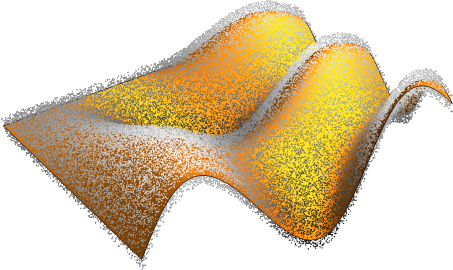

PhD and Bachelor Students

• Oliver Gäfvert (KTH): PhD student in algebraic and topological data analysis (coadvisor with Sandra Di Rocco and Wojciech Chachólski).
• Lukas Gustafsson (KTH): PhD student in algebraic geometry of data (coadvisor with Sandra Di Rocco and Kathlén Kohn).
• Frederik Möbius Rygaard: Bachelor's student in statistics on Riemannian manifolds (coadvisor with Steen Markvorsen and Søren Hauberg).

Publications

D. Kalatzis, D. Eklund, G. Arvanitidis, S. Hauberg, Variational Autoencoders with Riemannian Brownian Motion Priors (preprint).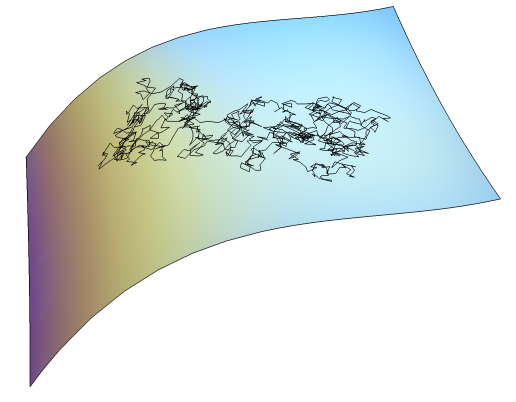
D. Eklund, S. Hauberg, Expected path length on random manifolds (preprint).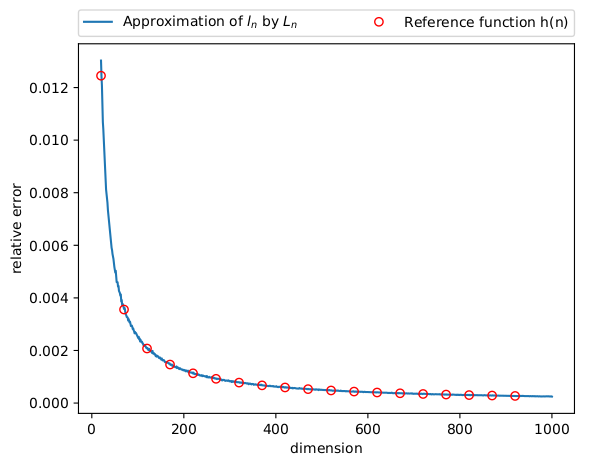
D. Bates, D. Eklund, J. D. Hauenstein, C. Peterson, Excess intersections and numerical irreducible decompositions (preprint).
S. Di Rocco, D. Eklund, M. Weinstein, The bottleneck degree of algebraic varieties (to appear in SIAM Journal on Applied Algebra and Geometry).
D. Eklund, The numerical algebraic geometry of bottlenecks (preprint). Some code.
S. Di Rocco, D. Eklund, C. Peterson, Numerical polar calculus and cohomology of line bundles, Advances in Applied Mathematics 100 (2018) 148-162.
D. Eklund, Curves on Heisenberg invariant quartic surfaces in projective 3-space, European Journal of Mathematics, 4(3), 931-952 (2018).
H. Abo, D. Eklund, T. Kahle, C. Peterson, Eigenschemes and the Jordan canonical form, Linear Algebra and its Applications, Volume 496, 121-151 (2016).
D. Bates, B. Davis, D. Eklund, E. Hanson, C. Peterson, Perturbed homotopies for finding all isolated solutions of polynomial systems, Applied Mathematics and Computation, Volume 247, 301-311 (2014).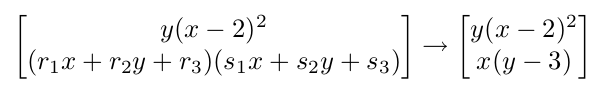
D. Bates, D. Eklund, C. Peterson, Computing intersection numbers of Chern classes, Journal of Symbolic Computation, Volume 50, 493-507 (2013).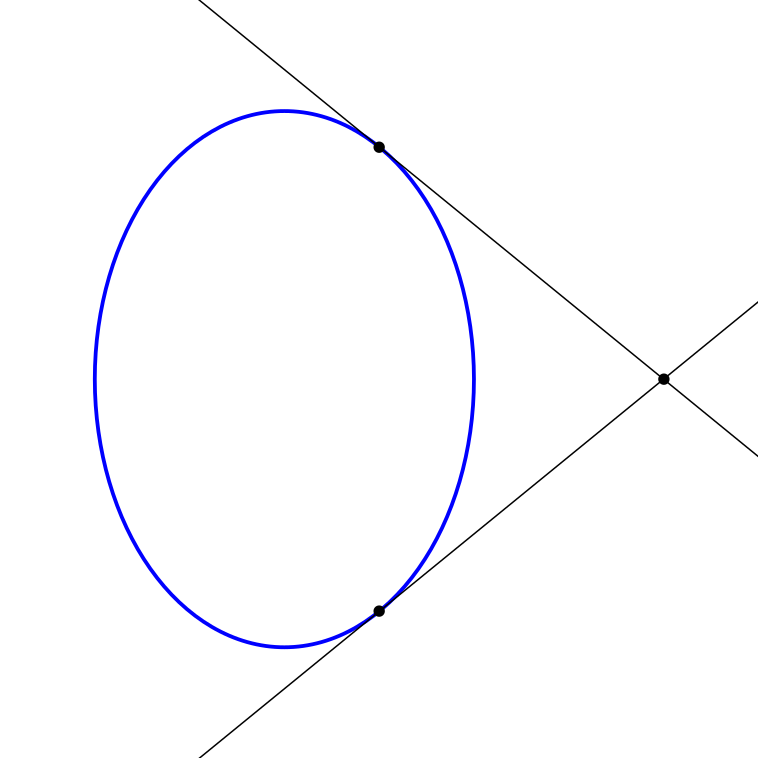
D. Eklund, C. Jost, C. Peterson, A method to compute Segre classes of subschemes of projective space, Journal of Algebra and Its Applications Volume 12, Number 2 (2013).
S. Di Rocco, D. Eklund, C. Peterson, A. Sommese, Chern numbers of smooth varieties via homotopy continuation and intersection theory, Journal of Symbolic Computation, Volume 46, Issue 1 (2011).
S. Di Rocco, D. Eklund, A. Sommese, C. Wampler, Algebraic C*-actions and the inverse kinematics of a general 6R manipulator, Applied Mathematics and Computation, Volume 216, Issue 9, 2512-2524 (2010).

The file robot.jpg is licensed under the Creative Commons Attribution-Share Alike 4.0 International license. Image created by Wikimedia Commons User Mgomezrobotnik. Image cropped and background color changed.