I am currently a visiting lecturer at Gothenburg University, lecturing at Chalmers Univeristy of Technology. Before this I was a postdoctoral researcher in probability theory at KTH Royal Institute of Technology, working with Fredrik Viklund and Jonatan Lenells. I finished my PhD at Chalmers University of technology in 2019, working together with Jeffrey E. Steif.

1. Wilson lines in the lattice Higgs model at strong coupling
   
   48 pages, 6 figures, (2022). With Jonatan Lenells and Fredrik Viklund
2. Wilson lines in the abelian lattice Higgs model
   
   53 pages, 7 figures, (2021).

1. Wilson loops in the abelian lattice Higgs model
   
   Accepted for publication in Probability and Mathematical Physics, 60 pages, 8 figures, (2022). With Jonatan Lenells and Fredrik Viklund.
   Source code for simulations
   

   

   
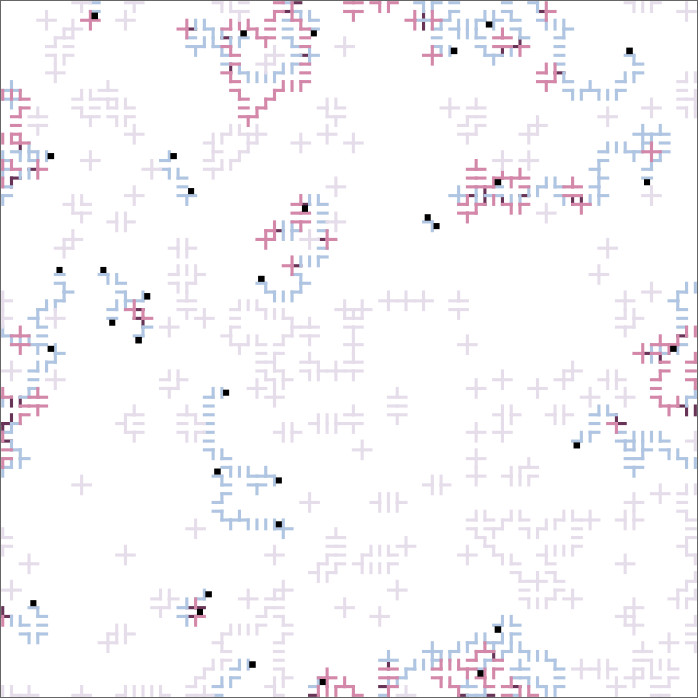
2. Decay of correlations in finite Abelian lattice gauge theories
   
   Communications in Mathematical Physics, 36 pages, (2022).
3. Wilson loops in finite Abelian lattice gauge theories.
   
   Accepted for publication in Annales de l'Institut Henri Poincaré (B) Probabilités et Statistiques, 37 pages, (2021). With Jonatan Lenells and Fredrik Viklund.
4. When are sequences of Boolean functions tame?
   
   Electronic Communications in Probability, Vol. 26, paper no. 64, 1-13, (2021).
5. A tame sequence of transitive Boolean functions.
   
   Electronic Communications in Probability, Vol. 25, paper no. 83, pp. 1-8, (2020).
6. Color representations of Ising models.
   
   Journal of Theoretical Probability, 33 pages, (2020).
7. A formula for hidden regular variation behavior for symmetric stable distributions.
   
   Extremes 23(4), pp. 667-691, (2020). With Jeffrey Steif.
8. Divide and color representations for threshold Gaussian and stable vectors.
   
   Electronic Journal of Probability, Vol. 25, paper no. 54, 45 pages, (2020). With Jeffrey Steif.
9. An analysis of the induced linear operators associated to divide and color models.
   
   Journal of Theoretical Probability, 18 pages, (2020) With Jeffrey Steif.
10. A few surprising integrals.
    
    Statistics and Probability Letters, Volume 157 , 4 pages, (2020). With Jeffrey Steif.
11. Denseness of volatile and nonvolatile sequences of Boolean functions.
    
    Stochastic Processes and their Applications, Vol. 128, Issue 11 (2018), pp. 3880--3896.
12. Monotonicity properties of exclusion sensitivity.
    
    Electronic Journal of Probability, Vol. 21, 22 pages, (2016), paper no. 45.
13. The spectrum and convergence rates of exclusion and interchange processes on the complete graph.
    
    Journal of Theoretical Probability, Vol. 30, Issue 2 (2017), pp. 639--654. With Johan Jonasson.
14. Exact Hausdorff measures of Cantor sets.
    
    Real analysis exchange, Vol. 39, No. 2 (2013-2014), pp. 367-384.

1. Wilson lines in the lattice Higgs model at strong coupling
   
   48 pages, 6 figures, (2022). With Jonatan Lenells and Fredrik Viklund
2. Wilson lines in the abelian lattice Higgs model
   
   53 pages, 7 figures, (2021).
3. A Noise Sensitivity Theorem for Schreier Graphs.
   
4. Noise Sensitivity and Noise Stability for Markov Chains: Existence Results.
   

• MVE580 Differential equations and linear algbra (Chalmers, 2022)
  
• LMA401 Analysis in one variable (Chalmers, 2022)
  
• SF2930 Regression Analysis (KTH, 2022)
  
  • Lecture 1
  • Lecture 4
  • Lecture 7
  • Lecture 11
  • Lecture 2
  • Lecture 5
  • Lecture 8
  • Lecture 12
  • Lecture 3
  • Lecture 6
  • Lecture 9
  • Lecture 13

• 2021: Ruth och Nils-Erik Stenbäcks stiftelse
  
• 2019: Kungliga vetenskapsakademin, Stiftelsen G S Magnusons fond
  
• 2015: Stiftelsen Olle Engkvist byggmästare
  
• 2014: SveFuM
  

• 2022-12: Quantization days 3.0
  

• 2022-08: Quantum Fields and Probability, Institut Mittag-Leffler
  
• 2022-08: 28th Nordic Congress of Mathematicians, Aalto University, invited session
  
• 2022-03: Percolation Today (together with Sky Cao)
  
• 2022-02: Durham Probability Seminar
  
• 2021-11: Grenoble Probability Seminar
  
• 2021-07: ICMP 2021: Young Researchers Symposium, invited talk
  
• 2021-05: CUNY Probability Seminar
  
• 2021-01: Spatial Networks and Percolation, Mathematisches Forschungsinsitut Oberwolfach
  
• 2020-11: Probability seminar, Chalmers University of Technology
  
• 2020-07: Women in Probability, Technical University of Munich, invited speaker
  
• 2020-03: Probability seminar, University of Stockholm
  
• 2020-02: Random matrix seminar, KTH Royal Institute of Technology
  
• 2019-06: 50 Years of the Random Cluster Model
  
• 2019-05: Probability seminar, KTH Royal Institute of Technology
  
• 2019-11: Uppsala probability seminar
  
• 2018-06: SPA 2018, contributed session