I am a Wallenberg Scholar, supported by the Swedish Research Council and the Göran Gustafsson Foundation.
Prior to returning to KTH, I was a Simons Fellow and Ritt Assistant Professor at Columbia University and then an associate professor at Uppsala University.
Editorial work: Arkiv för Matematik and Analysis and Mathematical Physics.
PhD students: Ellen Krusell, Vlad Guskov, Yan Luo (IHES, with Y. Wang), Lefteris Theodosiadis (with A. Sola, PhD 2024), Felix Rydell (with K. Kohn, PhD 2024), Lukas Schoug (PhD 2019).
Current postdocs: Levi Haunschmid-Sibitz, Mingchang Liu. Former postdocs: Erik Duse, Malin Palö Forsström, Atul Shekhar.
I am part of the Random Matrix Theory and Random Geometry (RMRG) research group at KTH.
We run a weekly seminar: The KTH Probability and Mathematical Physics Seminar. (Runs less frequently this semester due to the IML Program on Random Matrices and Scaling Limits.)
News and recent events
Call for postdocs in the RMRG group. Deadline is December 8, 2024. Please get in touch with me or Kurt Johansson if you are interested.
Helsinki-Stockholm Probability and Mathematical Physics days 2024, Nov 28-29, NORDITA, Stockholm.
Quantum fields, Probability and Geometry, Institut Mittag-Leffler Program, February-May 2027.
Quantum Fields and Probability II, Institut Mittag-Leffler, July 15-19, 2024.
New PhD course, Spring 2025: Teichmuller theory.
New PhD course (with A. Sola), Fall 2023 (course start Sept 13): Quasiconformal mappings in the plane
New PhD course given by L. Schoug, Fall 2023: Gaussian fields and random surfaces
Jeju Island Workshop 2023: Random conformal geometry and related fields in Jeju
MSRI Semester, Spring 2022: The Analysis and Geometry of Random Spaces.
Quantum Fields and Probability, Institut Mittag-Leffler, August 8-12, 2022.
Random growth: from lichen to lightning. Joint work with A. Sola and A. Turner made the cover of the London Mathematical Society Newsletter.
Research interests
My main areas of interest lie in complex analysis, probability, and mathematical physics, and especially problems where these areas meet. I am currently working on questions concerning Coulomb gases in the plane, the Loewner energy, Hele-Shaw flows, and lattice Yang-Mills theories.
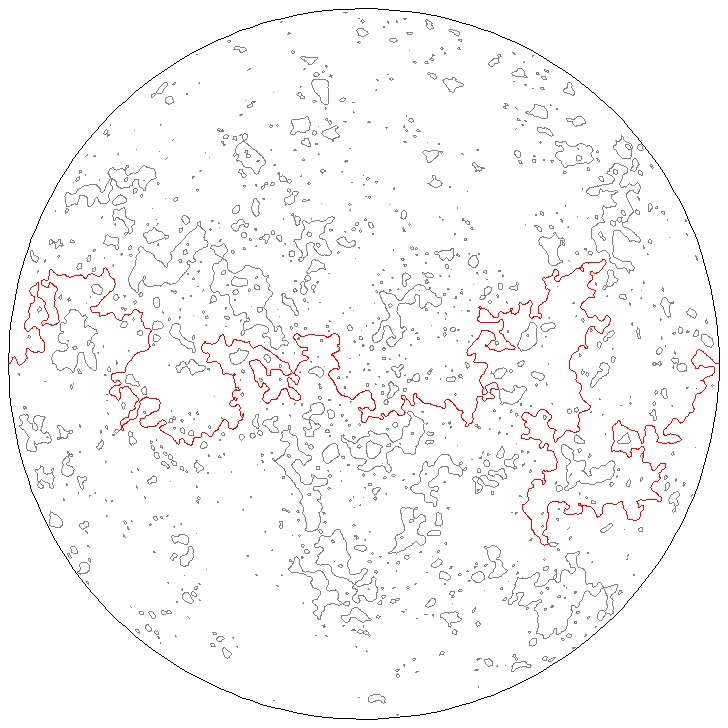
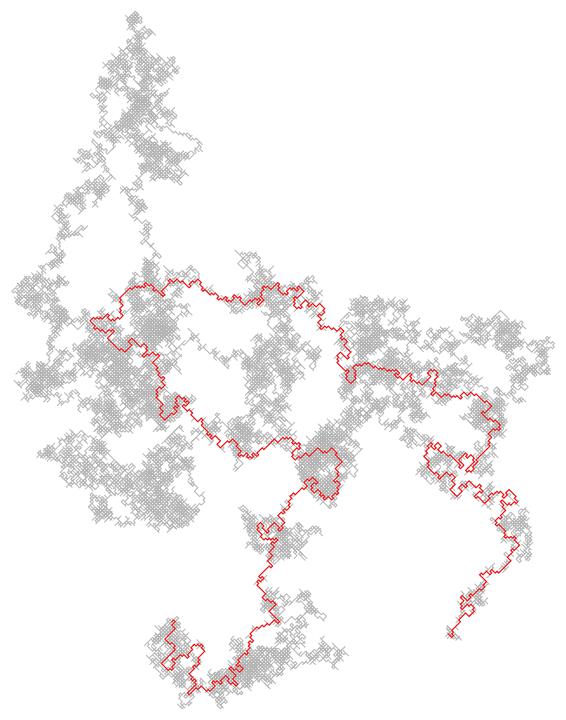
Other topics of (past and present) interest are fine geometric properties of Schramm-Loewner evolution (SLE) curves; scaling limits of critical lattice models; Laplacian growth and aggregation models; analytic and probabilistic aspects of conformal field theory. Pictures: A level line in a discrete Gaussian Free Field (courtesy of N.-G. Kang); a regularized Hastings-Levitov cluster with alpha=2; a loop-erased random walk derived from a 50k step simple random walk; a foliation of the unit disc generated by a measure with finite Loewner-Kufarev energy.
Papers
- Competitive Hele-Shaw flow and quadratic differentials
With D. Witt Nyström
[arXiv] - Coulomb gas and the Grunsky operator on a Jordan domain with corners
With K. Johansson
[arXiv] - Free energy and quark potential in Ising lattice gauge theory via cluster expansion
With M. P. Forsström
[arXiv] - Wilson lines in the lattice Higgs model at strong coupling
With M. P. Forsström, J. Lenells
Forthcoming in Ann. Appl. Probab.
[arXiv] - Percolation for two-dimensional excursion clouds and the discrete Gaussian free field
With A. Drewitz, O. Elias, A. Prevost, J. Tykesson
Forthcoming in Electron. J. Probab.
[arXiv] - The Loewner-Kufarev Energy and Foliations by Weil-Petersson Quasicircles
With Y. Wang
Proc. London Math. Soc. 128:2 (2024)
[arXiv] - Wilson loops in the abelian lattice Higgs model
With M. P. Forsström, J. Lenells
Probability and Mathematical Physics (PMP) 4 (2) (2023)
[arXiv] - Wilson loops in finite Abelian lattice gauge theories
With M. P. Forsström, J. Lenells
Ann. Inst. Henri Poincaré 58 (4) 2129-2164 (2022)
[arXiv] - Conformal Field Theory at the Lattice Level: Discrete Complex Analysis and Virasoro Structure
With C. Hongler, K. Kytola.
Comm. Math. Phys. 395 1--58 (2022)
[arXiv] [Journal]
-
Convergence of loop-erased random walk in the natural parametrization
With G. F. Lawler.
Duke Math. J. 170 (10) (2021)
[arXiv] [Journal] The Loewner difference equation and convergence of loop-erased random walk
With G. F. Lawler.
ALEA 19 (2022)
[Journal]
- Dimensions of two-valued sets via imaginary chaos
With L. Schoug, A. Sepulveda
Int. Math. Res. Not. (IMRN) 2022 (5) (2022)
[arXiv] [Journal] - Remarks on the regularity of quasislits
With L. Schoug, A. Shekhar
Ann. Acad. Sci. Fenn. Math 46 (1) (2021)
[arXiv] [Journal] - Interplay between Loewner and Dirichlet energies via conformal welding and flow-lines
With Y. Wang
Geom. Funct. Anal. (GAFA) 30 289–321 (2020)
[arXiv] [Journal] - Asymptotic analysis of Dotsenko-Fateev integrals
With J. Lenells
Ann. Henri Poincaré 20 (11) 3799-3848 (2019)
[arXiv] [Journal] - Schramm's formula and the Green's function for multiple SLE
With J. Lenells
J. Stat. Phys. 176 (4) 873–931 (2019)
[arXiv] - Transition probabilities for infinite two-sided loop-erased random walks
With C. Benes, G. F. Lawler. Electron. J. Probab. 24 Paper no 139, 22p (2019).
[arXiv] - One-dimensional scaling limits in a planar Laplacian random growth model
With A. Sola, A. Turner. Comm. Math. Phys. 371 (1) (2019)
[arXiv] [Journal] - Convergence of radial loop-erased random walk in the natural parametrization
With G. F. Lawler
[arXiv]
-
A dimension spectrum for SLE boundary collisions
With T. Alberts, I. Binder.
Comm. Math. Phys 348 (1) 273–298, (2016)
[arXiv]
-
Scaling limit of the loop-erased random walk Green's function
With C. Benes, G. F. Lawler.
Probab. Theory. Related Fields, 166 (1-2), 271–319 (2016)
[arXiv]
-
Small particle limits in a regularized Laplacian random growth model
With A. Sola, A. Turner.
Comm. Math. Phys. 334 (1), 331-366, (2015)
[arXiv] [Simulations]
-
Convergence rates for loop-erased random walk and other Loewner curves
Ann. Probab. 43 (1), 119-165 (2015)
[arXiv]
On the continuity of SLE(k) in k
With S. Rohde, C. Wong.
Probab. Theory Related Fields 159 (3), 413-433 (2014)
[arXiv]
-
Some remarks on SLE bubbles and Schramm's two-point observable
With D. Beliaev.
Comm. Math. Phys. 320 (2), 379-394 (2013)
[arXiv]
- Almost sure multifractal spectrum for the tip of an
SLE curve
With G. F. Lawler.
Acta Math. 209, 265-322 (2012)
[arXiv]
-
On the rate of convergence of loop-erased random walk to SLE(2)
With C. Benes and M. Kozdron.
Comm. Math. Phys. 308 (2), 307-354 (2013)
[arXiv]
-
Optimal Holder exponent for the SLE path
With G. F. Lawler.
Duke Math. J. 159 (3), 351-383 (2011)
[Journal] [arXiv]
-
Scaling limits of anisotropic Hastings-Levitov clusters
With A. Sola and A. Turner.
Ann. Inst. Henri Poincaré 48, 235-257 (2012)
[Journal] [arXiv]
-
On the scaling limit of loop-erased random walk excursion
Ark. Mat. 50 (2) (2012)
[Journal]
-
Random Loewner Chains
Doctoral Thesis from KTH Royal Institute of Technology, April 2010.
-
Rescaled Levy-Loewner hulls and random growth
With A. Sola.
Bull. Sci. Math. 133, 238-256 (2009)
[Journal] [arXiv]
Local activities
Informal summer school 2020: Grunsky operators, Fuchsian equations, inverse limits
Graduate course on geometric function theory, Fall 2020.
Selected topics in analysis: lattice models and random walk (new master's course), SF2716, Spring 2021.
Advanced complex analysis, SF2745 (new master's course), Spring 2020
KTH Probability Seminar (Since Spring 2023 merged with the Random Matrix Theory Seminar to form the Probability and Mathematical Physics Seminar.)
I was involved in a study group on Mathematics for Complex Data, Brummer & Partners MathDataLab.
Graduate course on Geometric Function Theory, Spring 2018.
Past events
Helsinki-Stockholm Probability and Mathematical Physics Days, Oct 26-27 2023, Helsinki.
MSRI Graduate Summer School, July 2021: Random Conformal Geometry.
Invited Session, SPA 2019, July 8-12, Evanston, IL, USA.
The analysis of Random Shapes, Jan 7-11, 2019, IPAM/UCLA, Los Angeles, CA, USA.
Invited Session, SPA 2018, June 11-15, 2018, Gothenburg, Sweden.
Random Conformal Geometry and Related Field, June 18-22, 2018, KIAS, Seoul, Korea. Funded by NSF, Samsung Science and Technology Foundation.
Mini workshop on Constructive Field Theory, March 13-15, 2018, Columbia University, NYC, USA. NSF funded.
Mini workshop on Log-Correlated Random Fields, Dec. 12-14, 2017, Columbia University, NYC, USA. NSF funded.
SLE, GFF and LQG in NYC, March 13-17, 2017, Columbia University, New York City, USA. NSF funded.
Institut Mittag-Leffler Workshop: Recent Developments in SLE, June 13-17, 2016, Djursholm, Sweden. Group photo.
One-day conference: Stockholm-Uppsala Analysis and Probability Day 2015, November 26, 2015, Uppsala, Sweden.
ICM Satellite meeting: Recent Progress in Random Conformal Geometry, August 11-12, Seoul, Korea.
One-day conference: Stockholm-Uppsala Analysis and Probability Day 2014, September 19, Stockholm, Sweden.
Travel
- June 10-21, 2019, Probability and quantum field theory, Porquerolles, France
- May 21-24, 2019, ETH Zurich
- Feb 2019, Workshop on statistical mechanics, Les Diablerets, Switzerland.
- Jan 7-12, 2019, Analysis and geometry of Random Shapes, IPAM workshop, UCLA, USA.
- March 12-17, 2018, Mini-workshop on Constructive Field Theory, Columbia University, New York, USA
- February 11-16, 2018, Topics in Geometric Function Theory, Les Diablerets, Switzerland
- January 18, 2018, Chalmers, Gothenburg
- December 10-16, 2017, Columbia University, NYC
- Nov 10-13, 2017, University of Bristol, University of Bath
- April 24, 2017, University of Geneva.
- March 19-21, 2017, MIT, Cambridge
- March 12-18, 2017, Columbia University, NYC
- January 24-25, 2017, IRS, Paris.
- December 14, 2016, Lund University.
- Oct 17-Nov 16, 2016, Columbia University.
- March 6-13, 2016, Everything is Complex, Saas Fee, Switzerland.
- April 4-8, 2016: UK Easter Probability Meeting. (Universtity of Lancaster.)