Förklaring
Laurentserier.

Det finns kanske anledning att fokusera uppmärkamheten på följande aspekter i kapitlet:

A. Tillåtna operationer på Taylorserier. (5.3 -5.4)

B. Konvergensradie och närmaste singularitet. (5.4 Thm 17)

C. Laurentserier och metoder att bestämma dem. (5.6)

D. Analytiska funktioners nollställen och analytisk fortsättning. (5.7)

A. Tillåtna operationer på Taylorserier.

När det gäller funktionsserier, alltså serier där termerna utgör funktioner av ex.vis en komplex variabel, uppstår problem som är relaterade till seriernas variabelberoende. Här är några exempel på gynnsamma egenskaper hos funktionsserier som man dock inte alltid kan räkna med:

1. Serien får integreras termvis.
2. Serien får deriveras termvis.
3. Serien får multipliceras termvis med en begränsad funktion.
4. Serien är analytisk, om termerna är analytisk.

Begreppet definieras i 5.3, där också Weierstrass' test för likformig konvergens formuleras.

Det viktigaste resultatet i detta sammanhang är dock att för de två typer av serier som är intressanta här, Taylorserier och Laurentserier, gäller att konvergensen alltid är likformig i det inre av konvergensområdet. (Thm 14, s. 234 resp. Thm 18, s. 264).

De 4 egenskaperna ovan gäller alltså för de serier som förekommer i kapitlet.

Dessutom kan tilläggas att absolutkonvergens också alltid gäller i det inre av konvergensområdet för dessa serier.

B. Konvergensradie och närmaste singularitet.

I komplex analys däremot utgörs konvergensområdena av cirklar och beteckningen konvergensradie blir mer begriplig.

I 5.4 visas detta (Thm 13) och begreppen konvergensradie och konvergenscirkel definieras.

Konvergensradien R kan precis som i det reella fallet vara oändlig, i vilket fall serien konvergerar för alla z.

Konvergensradien kan bestämmas med de metoder man minns från reella analysen: Kvot- eller rotkriteriet.
Dessa omnämns inte i 5.4 (jfr dock kvotkriteriet Thm 6 i 5.2, s.226) utan man ger ett mer lättillämpat villkor som fungerar i de fall man känner till den analytiska funktion f(z) som serien är en utveckling av:

Sats: Konvergensradien för en Taylorserie av f(z) omkring punkten z = z_o är lika med avståndet mellan z_o och f:s närmaste singulära punkt.

Detta formuleras på olika sätt både i Thm 15 och i Thm 17.

C.Laurentserier och metoder att bestämma dem.

c_n (z - z_o)ⁿ

P.g.a seriens dubbelsidighet (både positiva och negativa potenser) fordras normalt för konvergens att beloppet z-z_o varken är för stort eller för litet.
Det typiska konvergensområdet för en Laurentserie är därför ett ringformat område.

Mer detaljer om detta och om hur Laurentserier beräknas nås via länken till vänster.

Laurents sats (Thm 18) relaterar en Laurentserie till en analytisk funktion och anger att konvergensen mot funktionen är likformig i det inre av konvergensområdet.

En skillnad är dock att det oftast finns fler Laurentutvecklingar omkring en punkt z_o för en viss funktion och att dessa olika utvecklingar gäller i olika ringformade områden omkring z_o. (Se Ex 1-3, s, 268- 272 eller länken till vänster.)

I detta avsnitt krävs en viss förmåga att hantera serier, framför allt geometriska serier.
Utvecklingar som = 1 + t + t² +...       (t < 1 )
och 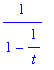= 1 +1/t + (1/t)² +...      (t > 1 )

kommer ofta till användning.

D. Analytiska funktioners nollställen och analytisk fortsättning.

Sats (Thm 19): Nollställena till en ickekonstant analytisk funktion är alltid isolerade.

Av detta följer i sin tur några entydighetsegenskaper:

Två analytiska funktioner f och g som är lika i en öppen mängd är lika i hela den gemensamma existensdomänen.

(Bilda skillnadsfunktionen s(z) = g(z) - f(z). Om g och f överensstämmer i en öppen mängd, får s(z) nollställen i en öppen mängd, vilket endast är möjligt om s(z) = 0 i hela existensdomänen.)

Om g:s existensdomän sträcker sig utanför f:s, kallas g(z) en analytisk fortsättning av f(z).

Ovanstående egenskap kan uttryckas även på följande sätt:
En analytisk fortsättning av en given funktion till en viss domän är unik.
(Ty om det finns två analytiska fortsättningar, bilda skillnadsfunktionen osv....) .

Även utvidgningar från kurvor, ex.vis reella axeln, är unika:

Om en reell funktion f(x) kan utvidgas till en analytisk funktion F(z) som överensstämmer med f(x) på den reella axeln, är denna analytiska utvidgning unik.
(Ty om det finns två olika utvidgningar F och G, bilda S = G - F. S måste då ha nollställen på hela reella axeln, vilket är omöjligt eftersom nollställena skall vara isolerade.)

• Gränsvärde av talföljd
• Partialsumma
• Oändlig summa som gränsvärde av partialsummorna.

• Absolut konvergens
• Betingad konvergens (conditional conv.)

Ex 2

Serier som konvergerar likformigt

• kan multipliceras termvis med en begränsad funktion (Thm 8)
• kan integreras termvis, om termerna är kontinuerliga (Thm 10)
• har en summa som är analytisk, om termerna är analytiska (Thm 11)
• kan deriveras termvis, om termerna är analytiska (Thm 12)
  s. 230-231

• Konvergenscirkel (Största cirkeln inom vilken en potensserie konvergerar överallt)
• Konvergensradie (Konvergenscirkelns radie)

En potensserie konvergerar likformigt på varje sluten cirkelskiva inom konvergenscirkeln. (Thm 14)

Sats: En analytisk funktion f(z) har en Taylorserie omkring z_o vars konvergensradie är lika med avståndet från z_o till närmaste singulära punkt.
Denna Taylorserie är den enda potensserie som konvergerar överallt mot f(z) inom konvergenscirkeln.(Thm 15 - 17)

Ex 3,4

13

21

• termvis derivering (Ex 1, s. 248)
• termvis integration (Ex 2, s. 248)
• bestämning av n:e-derivatan (Ex 3, s. 249)
  (Om funktionen är en gren av en flervärd funktion, måste motsvarande gren av derivatan väljas.)
• Multiplikation av serier (Ex 4, s. 250)
• partialbråksutveckling och utveckling av geometriska serier. (Ex 6, s. 254)

Ex 2

Ex 3

Ex 4

Ex 6

(*)         c_n (z - z_o)ⁿ

Laurents sats: En funktion, analytisk i ett ringformat område D: r₁ < z - z_o < r₂, kan representeras av en Laurentserie (*) i D,
där koefficienten c_n uppfyller
c_n = (C enkel sluten kurva i D).

Def: Isolerad singulär punkt.

Metod:Laurentutveckling m.hj.a. partialbråksutveckling och utveckling av geometriska serier. (Ex 1,2,3).

Ex 2

Ex 3

3

7

11

15

Def. Nollställets ordning

Sats (Thm. 19):
Nollställena till en ickekonstant analytisk funktion är alltid isolerade.

Följdsats (ej i kursboken):
Två analytiska funktioner som är lika i en öppen mängd eller på en ickedegenererad kurva är lika i hela den gemensamma existensdomänen.

Utvidgningen till en analytisk funktion f(z) från en reell funktion f(x) är alltså unik.

Def: En analytisk funktion som överensstämmer med en analytisk funktion f(z) i en öppen mängd, men existerar utanför f:s existensdomän, kallas en analytisk fortsättning av f(z).

En analytisk fortsättning av en funktion till en given domän är alltså unik.

Förklaring
Om väsentliga singulariteter.

6.1 Definition av residy.

Närmare bestämt residyn för f(z) i punkten z_o:

Res[ f(z), z_o ] = f(z) dz

Här antas att f(z) är analytisk på och inom den slutna kurvan C, utom i punkten z_o.

I samband med denna definition är det naturligt att erinra om möjligheten att Laurentutveckla f(z) omkring z_o:

f(z) = c_n (z - z_o)ⁿ

(där utvecklingen antas vara den serie som representerar f(z) i en punkterad omgivning av z_o)

samt om följande resultat från kapitel 4:

(z - z_o)ⁿdz =

Detta tillsammans med Laurentseriernas likformiga konvergens, som gör det möjligt att integrera f:s Laurentserie termvis, visar följande mycket viktiga relation:

f(z) dz = ( c_n (z - z_o)ⁿ ) dz = 2i c_-1.

Man får alltså (Thm 1, s.312 ):

Ofta används också (*) som definition av residyn för f(z) i z_o.

I Thm 2 (s. 314), som benämns residysatsen, formuleras en generalisering av (*) där den slutna kurvan C antas omsluta de n st. singulära ponkterna z₁, z₁, ... , z_n.

Man får då:

f(z) dz = 2i Res[f(z), z_k]

Beviset av residysatsen använder ett knep att modifiera integrationsvägarna som också används då deformationsprincipen visas.

Man likställer alltså integralerna längs kurvorna i figuren (fallet n=3) nedan

.

Eftersom summan av dessa integraler är 0 (inga singulariteter innanför C_U och C_L ) , blir summan av de fyra integralerna överst också 0. Omvändning av integrationsriktningarna i de tre inre cirkelintegralerna visar att summan av dessa (med positiv integrationsriktning) är lika med integralen över C, vilket skulle visas.

Observera att kursbokens cirkelintegraler på ett ställe (näst nedersta formeln på s. 315) har felaktigt angivna integrationsriktningar.

6.2 Isolerade singulariteter

Förgreningspunkter är alltså inte isolerade singulariteter.

Isolerade singulariteter kan klassificeras genom att man studerar Laurentutvecklingarna omkring dem.

En Laurentseries principaldel definieras som den del av serien som enbart innehåller negativa exponenter.

Om nu principaldelen till Laurentserien omkring z_o har ändligt många termer och den som har störst negativ potens är c_-N /(z-z_o)^N, kallas z_o en pol av ordning N till f(z).

OBS Med Laurentserien omkring z_o menas den Laurentutveckling som existerar i en punkterad omgivning av z_o och inte i någon annan cirkelring omkring z_o. Kursboken är litet oklar på den här punkten.

Om istället principaldelen till Laurentserien omkring z_o innehåller oändligt många termer och alltså har obegränsat stora negativa exponenter, kallas denna singulära punkt en väsentlig singularitet (essential singularity).

Def: Om en funktion som inte är definierad i z_o kan göras analytisk där med hjälp av en lämplig definition av f(z_o), kallas punkten z_o en hävbar singularitet (removable singularity).

Exemplet i boken, s.319, f(z) = (sin z)/z, är det klassiska exemplet på en hävbar singularitet i z = 0.

Avsnitt 6.2 avslutas med några metoder för att bestämma ordningen av en pol.

Den ledande idén är den som formuleras i RULE 1, nederst på s. 320:

Om z_o är en isolerad singularitet till f(z) och om
(z - z_o)^N f(z) existerar och inte är 0 (eller oändligheten),
så har f(z) en pol av ordning N i z_o.

De andra reglerna utgör i stort sett omformuleringar av samma sak.