Förklaring
Komplex parameterform

I 4.1 påminns man om den reella linjeintegralen

(*)        P(x,y)dx + Q(x,y)dy

x = x(t), y = y(t) , a t b. ,

i integralen så att följande reella enkelintegral uppstår:

(**)        (P(x(t),y(t))x'(t) + Q(x(t),y(t))y'(t))dt

Minnesregel:

• x och y övergår till x(t) resp. y(t)
• dx och dy övergår till x'(t)dt resp. y'(t)dt.

(***)        f(z)dz = (u+iv)(dx+idy) = (u+iv)dx + (iu-v)dy

Om integrationskurvan C är given på formen x=x(t), y=y(t) gör man precis som i avsnitt 4.1 för att överföra integralen till formen (**) som ju är en vanlig (dock komplexvärd) enkelintegral med en reell integrationsvariabel.

I avsnitt 4.2 beskrivs också den viktiga ML-olikheten, som används på flera ställen i resten av kursen.

Olikheten är enkel:

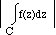
ML,

där M är en övre gräns för på C och där L är längden av C.

Beviset, som bygger på integralens definition, är bl.a. en tillämpning av triangelolikheten.

I avsnitt 4.3 införs komplexa integraler, definierade på s.k. styckvis släta kurvor (contours). Man kräver av sådana kurvor att de skall vara sammansatta av släta kurvor, dvs. kurvor vars parameterfunktioner är deriverbara och där derivatorna ej samtidigt är 0.(s. 143).

De komplexa linjeintegraler för vilka integrationskurvan är sluten betecknas ofta

f(z)dz

där pilen anger omloppsriktning.
Positiv omloppsriktning kan som vanligt beskrivas av adverbet 'moturs'.

För sådana slutna linjeintegraler är det naturligt att tillämpa Greens formel:

Pdx + Qdy = (Q_x - P_y)dxdy

där C är en sluten kurva med positiv omloppsriktning som innesluter D.

Denna formel fordrar som bekant att P och Q samt deras derivator är kontinuerliga på C och i D.
Om man tillämpar denna formel på den komplexa linjeintegralen (***),
där alltså P = u + iv och Q = iu - v får man som integrand i dubbelintegralen
Q_x - P_y = iu_x - v_x -(u_y + iv_y = -v_x - u_y + i(u_x - v_y).

Här känner man igen Cauchy-Riemanns ekvationer!
Dvs. om C-R-ekvationerna gäller, så blir Q_x - P_y = 0.

Så att om f(z) är analytisk i D och på C (och om f'(z) är kontinuerlig där så att Greens formel får tillämpas) så får man följande slående resultat (Cauchy-Goursats sats, s.162):

(#)        f(z)dz = 0

för alla sådana slutna kurvor C.

Ur (#) får man tämligen direkt också deformationsprincipen som innebär att

f(z)dz = f(z)dz,

om C₁ och C₂ är slutna kurvor så att hela C₂ ligger i det inre av C₁ och om f(z) är analytisk på C₁ och C₂ samt i den ringformade domän som ligger mellan C₁ och C₂.

Från teorin om reella linjeinegraler minns man att om en viss linjeintegral är 0 för alla slutna integrationskurvor, så är linjeintegralerna med denna integrand mellan två punkter oberoende av vägen mellan punkterna.

Kriteriet för detta i det reella fallet är ju Q_x - P_y = 0, då linjeintegralens integrand är Pdx + Qdy.
För komplexa linjeintegraler med analytiska integrander är som vi har sett motsvarande kriterium alltid uppfyllt p.g.a. Cauchy-Riemann-ekvationerna. Denna oberoende-av-vägen-princip gäller alltså generellt för analytiska funktioner (Thm 4, 4.4).

Om startpunkten z_o för en integrationskurva är fix, blir p.g.a denna princip komplexa integraler f(z) dz längs kurvor mellan z_o och z endast beroende av z.
Detta leder till att man kan definiera analytiska primitiva funktioner med hjälp av sådana integraler vilket leder till en metod att bestämma komplexa integraler via primitiva funktioner (Thm 5, 4.4) eftersom en komplex version av integralkalkylens fundamentalsats (derivatan av en integral m. avs. på övre gränsen är lika med integranden) kan visas gälla (Thm 6, 4.4).

Det är dock viktigt att all integration sker inom integrandernas analycitetsdomäner.
Och om integrationsvägen mellan två punkter byts, får det inte finnas någon singularitetspunkt mellan den gamla och den nya vägen.

I Cauchy-Goursats sats spelar satsens exakta förutsättningar en viss historisk roll: Cauchy härledde formeln och Goursat lyckades visa den utan Greens formel och utan att använda förutsättningen att f'(z) skall vara kontinuerlig.
Detta har en stor betydelse eftersom formeln (#) i och med det kan användas till att visa att f'(z) alltid är kontinuerlig om f(z) är analytisk.
Och inte bara det.
Man kan visa från (#) att om f(z) är analytisk så har f(z) derivator av obegränsat hög ordning!

Dessa resultat visar sig följa av den viktiga formel som härleds i 4.5:

Cauchys integralformel:

_{(##)       f(zo}) =

I beviset för (##) används utöver (#) också resultatet

= 2i.

där C är någon kurva som omsluter z_o.

Här kan man p.g.a.deformationsprincipen låta C vara en cirkel med centrum i z_o.

På s. 162 - 163 härleds det allmännare resultatet att

(z - z_o)ⁿdz =

Kursbokens bevis av (##) använder också ML-olikheten samt följande generella princip:

Om < för alla > 0, så måste w = 0.

Cauchys integralformel kan generaliseras till följande formel som gäller för en godtycklig n:e-derivata f⁽ⁿ⁾(z) av en analytisk funktion f:

_{(###)       f⁽ⁿ⁾(zo) =}

Det är denna generaliserade integralformel som visar att om f är analytisk (dvs. deriverbar en gång i någon öppen mängd) så är f obegränsat deriverbar.
Formeln ger ju n:e-derivatan i z_o som en existerande integral i termer av f(z) enbart.

Allt detta står i skarp kontrast till motsvarande förhållanden inom teorin för reella funktioner.
Där förekommer funktioner som är deriverbara n gånger i en punkt men där (n+1):a derivatan inte existerar.
F(x) = ^35/2 är exempelvis deriverbar 17 gånger i x=0 men inte 18.

Kapitel 4 avslutas i avsnitt 4.6 med några tillämpningar av Cauchys integralformel.

Gauss' medelvärdessats följer direkt av denna integralformel om man låter C vara en cirkel med centrum i z_o med radien r och inför det reella argumentet som integrationsvariabel:

f(z_o) = f(z_o + reⁱ)d

Högerledet utgör medelvärdet av f:s värden på cirkeln.

Det är en viktig och remarkabel egenskap hos analytiska funktioner att funktionsvärdena alltid utgör komplexa medelvärden av funktionsvärdena på omgivande cirklar.

En besläktad egenskap formuleras av Maximum modulus-satsen (Thm 12, 4.6): Om f(z) är analytisk i en begränsad domän D och kontinuerlig i D:s slutna hölje R (dvs i området bestäende av D och D:s rand) , så antar sitt maximum inom R på randen.

Liouvilles sats (Thm 13, 4.6) säger att om en hel funktion har ett belopp som är begränsat, så måste funktionen vara konstant. Se förklaringen till vänster om hur detta följer av Max.mod-satsen samt om hur Liouvilles sats kan användas för att bevisa Algebrans fundamentalsats.

ML-olikheten s.155

Ex 4

(z - z_o)ⁿdz =

Deformationsprincipen (Thm 3-4)

Ex 2
Ex 3

25

Komplex integration m.hj.a. primitiva funktioner (Thm 5)

Integralkalkylens fundamentalsats för analytiska funktioner(Thm 6)

11

Cauchys integralformel för f⁽ⁿ⁾ (Thm 8)

13

Maximum modulus-satsen(Thm 11)

Liouvilles sats (Thm 13)
Beviset av Algebrans fundamentalsats (s. 196)

15