Teckenstudium

Här tränas teckenstudium av polynom och rationella funktioner (som är kvoter av polynom). Metoden går ut på att man faktoriserar funktionen så långt som möjligt och därefter systematiskt studerar funktionens tecken genom att sammanställa faktorernas tecken i en tabell. ( Se Exempel 1 och SfS-exemplet.)

Observera särskilt de kolumner som svarar mot intervall. man kan alltså studera funktionens tecken för alla x i olika intervall. Detta gör dessa teckentabeller klart överlägsna de punkttabeller som man ibland kan göra som stöd för en grafskissering: Här kan man ju inte uttala sig om hur funktionen uppför sig mellan punkterna.

En del av problemet består i att utföra faktoriseringen.
Man måste kunna sätta funktionen på gemensamt bråkstreck och faktorisera m.hj.a polynomdivision om något av detta behövs.

En vanlig tillämpning är att fastställa derivatans tecken i samband med kurvundersökningar.

Definitionsmängder

Teckenstudium är också ett viktigt inslag i hanteringen av funktioner med begränsad definitionsmängd. De funktioner av denna typ man först brukar stöta på är kvadratroten och logaritmerna. Följande inskränkningar gäller:

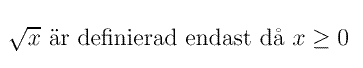
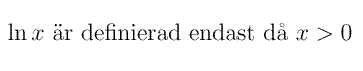
och man får ju inte heller glömma:

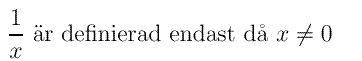
En del av problemen i detta avsnitt är formulerade som bestämningar av definitionsmängder. Men det handlar alltså egentligen om vanligt teckenstudium av rationella funktioner.

Grafer

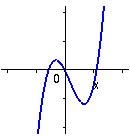
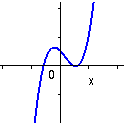
y = x(x+1)(x-2)	y = (x+1)(x-1)2	Till vänster visas grafen av ett tredjegradspolynom på faktoriserad form, vilket gör det möjligt att avläsa nollställenas läge. Kontrollera att varje faktor av typ (x-a) svarar mot nollstället x=a! Till höger visas grafen av ett tredjegradspolynom med en kvadratisk faktor (x-1)2. Detta svarar mot arr x=1 är ett dubbelt nollställe till polynomet. Man ser också att funktionsvärdena är > 0 på båda sidor av x=1, vilket är typiskt för kvadratiska faktorer. I teckentabellen hade man fått kombinationen ' + 0 + ' omkring x=1.
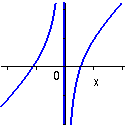y = r(x) = (x-1)(x+2)/x	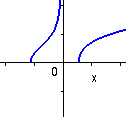y = kvadratroten ur r(x),	Till vänster visas grafen av en typisk rationell funktion, r(x), som växlar tecken i x=-2, 0 och 1. I x=0 finns dessutom en lodrät asymptot på grund av nämnarens nollställe x=0. Till höger visas kvadratroten ur samma funktion. Man ser att denna funktions definitionsmängd endast omfattar de x för vilka r(x) inte är < 0.