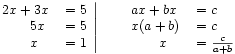Bråkstreck

• Gemensamt bråkstreck. Två fall:
  • Ingen gemensam faktor i nämnarna (Ex: )
        Se Exempel 1

  • Gemensam faktor i nämnarna (Ex: )
        Se Exempel 2

• Huvudbråkstreck. Två fall: ,   Se Övning 1d  , och   

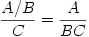
Ekvationslösning

• Observera följande skillnad mellan ekvationslösning utan resp. med parametrar:
  

  I det senare fallet behöver man alltså införa en parentes och bryta ut variabeln x för att komma vidare. Se Exempel 3

• Bråkstreckshantering i ekvationer: Ibland är det gynnsamt att sätta uttryck på gemensamt bråkstreck i ekvationer och ibland inte.
  Övning 2b är ett exempel på att gemensamt bråkstreck behövs, medan
  Övning 2a visar ett fall då detta inte behövs (p.g.a. nollan i högerledet).

Grafer

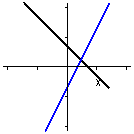
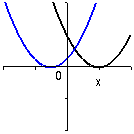
y = ax + b	y = (x-c)2	Parameteruttryck i x och y ska man se som en mängd av kurvor där parametervärdena påverkar kurvornas utseende. Till vänster står y = ax + b för en mängd räta linjer där a anger linjens lutning. Två exempel är plottade (y=-x + 1 och y=2x - 1 ). Till höger ser man två representanter för parablerna som kan skrivas y = (x-c)2. (y=(x+0.5)2 och y=(x-1)2). Här anger c läget på x-axeln för parablernas minimipunkter.
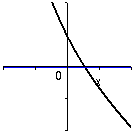y = e-x - x	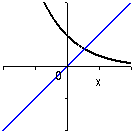y = e-x,    y = x	Exemplen visar hur en lösning till en ekvation kan representeras grafiskt på olika sätt. Till vänster ser man hur roten till ekvationen y = e-x - x = 0 framtråder som x-koordinaten för skärningspunkten mellan funktionsgrafen för y = e-x - x och x-axeln. Till höger har graferna för y = e-x och y = x plottats och lösningen till samma ekvation återfinns som x-koordinaten för de två grafernas skärningspunkt.