Vi närmar oss nu slutet av kursen.
Avsnitt 4, som består av kapitel 6 och 7 i Vretblad, handlar om komplexa tal.
Kommentarerna handlar i tur och ordning om
- Andra- och tredjegradsekvationerna och de komplexa talen.
- Grupper, ringar och kroppar
- Kommentarer till ISU:erna
- Lösningar till uppgifterna 627 och 628 (sid. 126)
Andra- och tredjegradsekvationerna och de komplexa talen.
Kapitel 6 ger en introduktion av de komplexa talen, där man lär sig att handskas med konjugering, division, absolutbelopp. polär form osv. De Moivres formel skall heller inte glömmas.
Dessutom lär man sig att lösa andragradsekvationer och binomiska ekvationer.Vad gäller andragradsekvationer så kommer de komplexa talen till en naturlig användning när man råkar ut för ett negativt tal under rottecknet.
Exempel: x2 + 2x + 5 = 0 ger
 .
.
Däremot är det inte lika klart hur man handskas med ekvationer som redan innehåller det imaginära talet 'i'.
Exempel: x2 + 2x + 5 - i = 0 ger enligt samma lösningsformel:
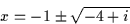 ,
,
vilket dock inte är ett tillfredsställande svar eftersom 'i' återfinns under rottecknet.
Hur man löser detta problem framgår av Vretblad kap. 6.5. (Se exempel 1, sid. 422).Historiskt sett har de komplexa talen haft det något motigt då det gäller att bli accepterade inom matematikerkretsar. Först en bit in på 1800-talet förefaller dessa tal ha vunnit allmänt erkännande. Även den store matematikern Gauss 1777-1855 var åtminstone i början av sin karriär obenägen att fullt ut förlita sig på dessa kontroversiella storheter även om han insåg deras betydelse.
Tidigare hade de komplexa talen haft ett slags skuggtillvaro som mer eller mindre suspekta hjälpmedel för att lösa vissa problem.Ett sådant problem, troligen det första där de komplexa talen skulle visa sig vara oundgängliga, uppstod i samband med försöken att lösa tredje- och fjärdegradsekvationerna.
Det kan ha ett visst intresse att titta litet närmare på detta i fallet tredjegradsekvationen.
En tredjegradsekvation med reella koefficienter har antingen tre reella rötter eller också en reell rot (samt två konjugerat komplexa rötter). I det första fallet uppstår en svårighet med den lösningsmetod som upptäcktes redan på 1500-talet av några italienare (del Ferro, Cardano m.fl.). Vad dessa skickliga matematiker råkade ut för, och som säkerligen satte myror i huvudet på dem, var följande effekt, som jag beskriver genom ett konkret exempel:
-
Betrakta ekvationen x3 - 6x + 4 = 0 .
- (1 + i)3 = 1 + 3i - 3 - i = -2 + 2i, varför
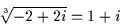
- Analogt, (1 - i)3 = 1 - 3i - 3 + i = -2 - 2i, varför
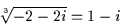
Summan blir alltså (1 + i) + (1 - i) = 2.
- Analogt, (1 - i)3 = 1 - 3i - 3 + i = -2 - 2i, varför
Vid lösningen av denna ekvation m.hj.a. den vanliga lösningsmetoden uppträder följande rotuttryck:
 ,
,
som med användande av talet 'i' kan skrivas:
Motivering: .
.
Nu kan man inse (vilket också redan Cardano gjorde) att detta rotuttryck faktiskt är lika med 2.
Och just detta problem anses numera som en av de historiskt viktigaste drivkrafterna för införandet av (eller om man så vill, upptäckten av) de komplexa talen.
Det mirakulösa i sammanhanget är att man överhuvudtaget klarade av att lösa tredjegradsekvationer så länge utan komplexa tal.Titta gärna på lösningsformeln .
Den omnämns ofta men visas sällan.Grupper, ringar och kroppar.
Kapitel 7 handlar om egenskaper hos polynom. Här är det väsentligt att känna till de komplexa talen.Man märker till sin glädje(?) att tankegångar från kapitel 2 (Egenskaper hos heltalen) återkommer här. Division av polynom är lika viktig som division av hela tal (och utförs på liknande sätt). Dessutom återkommer Euklides algoritm i en polynomversion.
Denna likhet mellan hela tal och polynom studeras i abstraktare versioner av algebra än vad som behandlas i den här kursen. Där finner man begreppet ring som har en specifik matematisk betydelse. En ring är ett algebraiskt system som uppfyller ringaxiomen. Dessa axiom (som inte specificeras närmare här) innehåller regler för operationerna addition och multiplikation och det visar sig att både heltal och polynom uppfyller dessa axiom. Man säger att både heltalen och polynomen (av en variabel, två variabler osv. ) utgör ringar. Men även en mängd andra matematiska strukturer visar sig vara ringar.
Detta att definiera en klass matematiska system med hjälp av ett axiomsystem är en typiskt fruktbar matematisk idé som ofta återkommer på litet högre nivåer. Metoden ger exempelvis möjlighet att urskilja vad som är allmänna 'ringegenskaper' hos polynom och hela tal och vad som är specifika egenskaper som skiljer polynom från heltal
Jag tar upp det här med ringar av en viss anledning och det har att göra med benämningen på kursen: Algebra.
I vida kretsar betraktas nämligen algebra som studiet av s.k. algebraiska strukturer varav grupper, ringar och kroppar brukar anses vara de viktigaste. Ni kan alltså råka ut för den litet förargliga situationen att betraktas som specialister på sådana strukturer trots att de inte omnämns alls i Vretblads kursbok. Nå, detta är ju en inledande kurs och abstraktionerna är därmed inte drivna så långt. Men vi kan ju ändå hävda att det förekommer ringteori i kursen i och med att både hela tal och polynom studeras.Vad gäller kroppar så är både de rationella talen , de reella talen och de komplexa talen exempel på sådana strukturer och de har ju också förekommit i kursen.
Grupper, slutligen har däremot inte figurerat så mycket i kursen. Det är strukturer med bara en operation definierad och de dök upp första gången i historien vid studiet av ekvationer. De användes exempelvis i beviset av att 5:egradsekvationer och högre ordningens ekvationer inte kan ha lösningsformler av den typ som 2:a- ,3:e- och 4:egradsekvationerna har.
Ett exempel på en grupp får man om man betraktar de hela talen och glömmer bort multiplikationsoperationen. De positiva reella talen med addition bortglömd bildar också en grupp. Även ändliga grupper (dvs. grupper med ändligt många element) förekommer och studeras mycket. Här är en historisk länk om gruppteorins utveckling.. Läs gärna vidare om dessa ting i biografierna över Abel och Galois. De är så märkliga att de även har allmänt, utommatematiskt intresse.Kommentarer till ISU:erna.
- Räkning med 'i'. Exemplet överst på sid. 113 säger allt.
- Här behövs litet förenkling först (i a och b) som i uppgift 1.
Sedan använder man bara definitionen på absolutbelopp.
I c) behöver man erinra sig litet trigonometri, exempelvis formlerna
cos2v + sin2v = 1 och cos2(v/2) = (1 + cosv)/2 . - Här har man hjälp av Läsanvisningarnas Exempel överst på sid.3 i Avsnitt 4.
Även de Moivres formel behöver användas för att ta hand om de höga exponenterna 75 resp. 22.
Här måste man också komma ihåg sinus och cosinus för våra vanligaste vinklar, som/6,
/4 och
/3.
Och vi använder förstås radianer som vinkelmått,
Minnesregel:radianer svarar mot 180 grader.
- Vretblads lösning av ekvation (*) på sid. 123 ger bra ledning.
Metod 2 på sid. 122 fungerar bra i andra steget av lösningen. - Detta är en binomisk ekvation och löses med den metod som beskrivs på sid. 124-125.
- Här bör man alltså lära sig polynomdivision enligt någon metod. (Två förslag finns på sid. 132). Gissningen är inte alltför svår och dessutom finns ju facit...
- Här är alltså den gamla bekanten SGD tillbaka fast i polynomversion. Men Euklides algoritm kan man känna igen, se sid. 138.
- Ungefär som uppgift 6, men man behöver tillämpa Sats 8.
- Åter ett fall för Sats 8. Se även Exemplen på sid. 140 (gäller även uppgift 8).
- Liknar uppgift 6, men man behöver nog hjälp med gissningen av Sats 11.
- Liknar mycket Exempel 1 på sid. 142. Detta är första (och sista) gången i kursen man behöver kunna derivera!
- Grupper, ringar och kroppar