Tredjegradsekvationen
Först inser man att den allmänna tredjegradsekvationen(1) az3 + bz2 + cz + d = 0
(2) x3 + px + q = 0
genom substitutionen z = x - b/(3a).
Så det räcker alltså att ange lösningen till ekvation (2).
Inför nu beteckningarna
D = (p/3)3 + (q/2)2.
och
.
De tre rötterna x1, x2 och x3 kan då uttryckas på följande sätt:
Exempel:
x3 - 6x + 4 = 0
Här är p = -6, q = 4 samt D = (-6/3)3 + (4/2)2 = -8 + 4 = -4.
Man får som visats tidigare i huvudtexten: u = 1 + i och v = 1 - i , varav
x1 = 2,
x2 = -1 + i2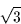
= -1 - 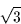samt
x3 = -1 - i2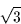 = -1 + .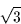