This work investigates video coding with wavelet transforms applied in the temporal direction of a video sequence. The wavelets are implemented with the lifting scheme in order to permit motion compensation between successive pictures. We improve motion compensation in the lifting steps and utilize complementary motion-compensated signals. Similar to superimposed predictive coding with complementary signals, this approach improves compression efficiency. We investigate experimentally and theoretically complementary motion-compensated signals for lifted wavelet transforms. Experimental results with the complementary motion-compensated Haar wavelet and frame-adaptive motion compensation show improvements in coding efficiency of up to 3 dB. The theoretical results demonstrate that the lifted Haar wavelet scheme with complementary motion-compensated signals is able to approach the bound for bit-rate savings of 2 bits per sample and motion-accuracy step when compared to optimum intra-frame coding of the input pictures. (Article)

1. Haar Wavelet with Complementary Motion-Compensated Signals

The classic motion-compensated Haar wavelet permits motion compensation in the prediction and update steps of the lifting structure. The motivation for motion compensation in the lifting steps is to perform a wavelet transform along the motion trajectories in a video sequence for more efficient decorrelation of successive pictures. As the true motion in a video sequence is not known a priori, the encoder is bound to utilize only an estimate of the motion for compensation in the lifting steps. Efficient motion compensation relies on accurate motion estimates. But any practical coding scheme has to deal with inaccurate motion compensation due to quantization of motion information. One approach to encounter the degradation due to inaccurate motion compensation is to utilize complementary motion-compensated signals. The rationale for this approach is to accept the degradation of one inaccurate motion-compensated signal but to combine it with at least another inaccurate motion-compensated signal such that the superimposed signal causes less degradation than each individual signal will inflict. Therefore, we extend the motion compensation in the prediction and update steps of the Haar wavelet such that we are able to utilize complementary motion-compensated signals in the lifting steps.

The figure depicts an example of the adaptive Haar wavelet where N=2 motion-compensated signals with estimated displacements are averaged in the prediction step as well as in the update step. Note that we utilize for the update step just the negative vectors of the estimated displacement vectors in the prediction step. This is the best choice if the motion field between the two pictures is invertible. Otherwise, we obtain just a suboptimal approximation with low computational complexity.

2. Experimental Results

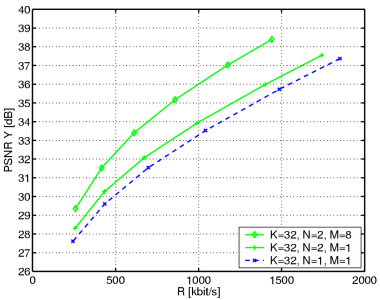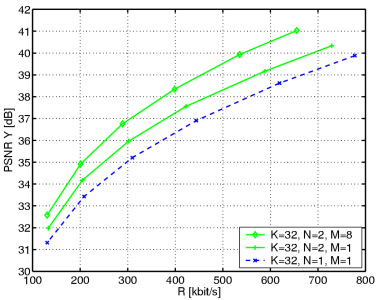
The figures show the luminance PSNR over the total bit-rate for the sequences Foreman (left) and Mobile & Calendar (right). We subdivide the sequences, each with 288 frames, into groups of K=32 pictures and encode them with the complementary motion-compensated Haar wavelet. The classic Haar wavelet with one motion-compensated signal (N=1) and one "reference" picture (M=1) provides the reference performance. Choosing N=2 complementary motion-compensated signals from M=1 picture provides an improvement in compression efficiency of up to 1 dB. Permitting frame-adaptive motion compensation with up to M=8 even pictures improves the efficiency up to 3 dB for the investigated test sequences. Please note the relation to the 5/3 wavelet in the case N=2 and M=2: If one of the two motion-compensated signals is always chosen from the previous even picture and the other from the subsequent even picture for all blocks in the odd picture, we obtain the classic motion-compensated 5/3 wavelet.

3. Signal Model for Haar Wavelet with Complementary Motion-Compensated Signals

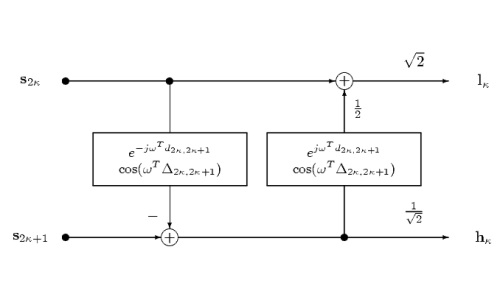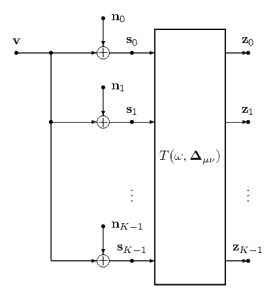Consider the complementary motion-compensated Haar wavelet in left figure. We assume that the prediction step averages N=2 motion-compensated signals. Further, the true displacements are identical for both motion-compensated signals. As we assume ideal complementary signals, the variances of both displacement errors are identical and the correlation coefficient is maximal negative. With the definition of the true displacement, the transfer functions of prediction and update step are characterized by the cosine of the displacement errors.

The right figure shows the model for the input pictures s and the motion-compensated transform T which is dependent on the displacement errors. The output pictures z are independently intra-frame encoded. Note that true displacements which are non-zero do not influence the performance of the optimal intra-frame encoder.

4. Transform Coding Gain

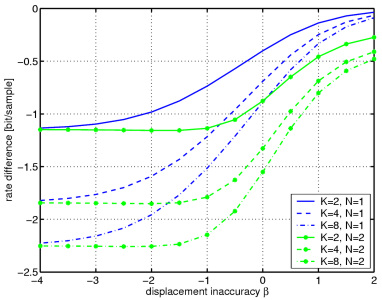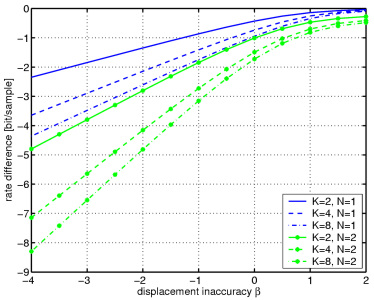
The figures depict the overall rate difference for the Haar wavelet with motion compensation (N=1) and N=2 complementary motion-compensated signals over the displacement inaccuracy for a residual noise level of -100 dB (left) and -30 dB (right). The variance of the video signal v is normalized to 1. The bounds for the complementary motion-compensated Haar wavelet (N=2) are shown for K=2,4, and 8. Note that the complementary motion-compensated Haar wavelet (N=2) achieves a rate difference up to 1 bit per sample and motion-accuracy step already for a GOP size of K=2, whereas for N=1, a very large GOP size is required to achieve this slope. On the other hand, the results for N=2 suggest that a rate difference of up to 2 bits per sample and motion-accuracy step is feasible for a very large GOP size. In the presence of residual noise, both approaches with the same GOP size K converge for very accurate motion compensation to the same rate difference as we assume identical residual noise levels.

This work investigates video coding with wavelet transforms applied in the temporal direction of a video sequence. The wavelets are implemented with the lifting scheme in order to permit motion compensation between successive pictures. We generalize the coding scheme and permit motion compensation from any even picture in the GOP by maintaining the invertibility of the inter-frame transform. We show experimentally, that frame-adaptive motion compensation improves the compression efficiency of the Haar and 5/3 wavelet. (Article)

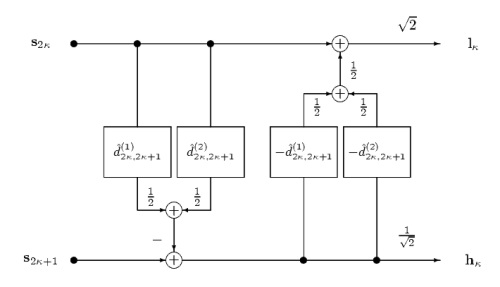
1. Lifted Haar Wavelet and Frame-Adaptive Motion Compensation

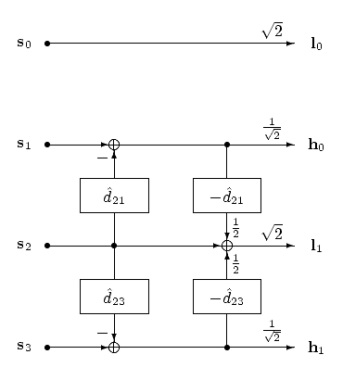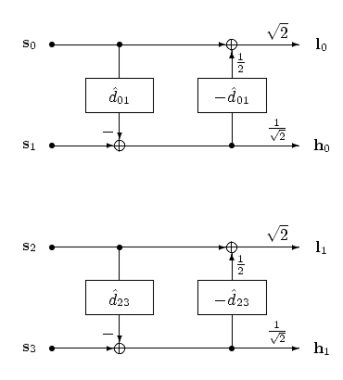
The left figure depicts the Haar transform with motion-compensated lifting steps. The even frames of the video sequence are displaced by estimated displacements to predict its odd frames. The prediction step is followed by an update step with the negative estimated displacements. For frame-adaptive motion compensation, we go one step further and permit at most M even frames to be reference for predicting each odd frames. In the prediction step, we select for each block in the frame one motion vector and one picture reference parameter. The picture reference parameter addresses one of the M even frames in the GOP and the update step modifies this selected frame. Both motion vector and picture reference parameter are transmitted to the decoder. As we use only even frames for reference, the inter-frame transform is still invertible. The right figure depicts the example where frame s₂ is used to predict frame s₁. If parts of an object in frame s₁ are covered in frame s₀ but not in frame s₂, the selection of the later will avoid the occlusion problem and, therefore, will be more efficient. Note that for each block, the reference frame is chosen individually.

2. Experimental Results

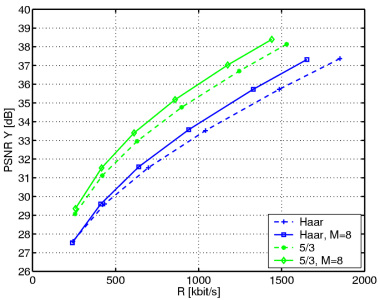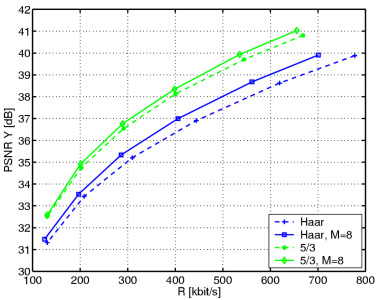
The figures show the luminance PSNR over the total bit-rate for the QCIF sequences Foreman (left) and Mobile & Calendar (right) at 30 fps. We subdivide the sequences, each with 288 frames, into groups of K=32 pictures and encode them with the 5/3 kernel. We utilize a set of M=8 reference frames to capture the performance of the frame-adaptive motion-compensated transform. For reference, the performance of the scheme with fix reference frames is given (5/3). The performance of the Haar kernel with fix reference frames (Haar) and frame-adaptive motion compensation (Haar, M=8) is also plotted. We observe for both sequences, that the 5/3 kernel outperforms the Haar kernel and that frame-adaptive motion compensation improves the performance of both. In any case, the gain in compression efficiency grows with increasing bit-rate.

This work investigates lifted Wavelet transforms applied in the temporal direction of a video sequence. Due to the motion between pairs of frames, motion compensation is utilized in the lifting steps. We discuss the modified Haar and 5/3 wavelet kernel and provide experimental results for dyadic decompositions with various levels. Further, we utilize a signal model for a theoretical discussion of both kernels. We generalize and replace the dyadic decompositions by the Karhunen-Loeve Transform in order to provide theoretical performance bounds for the compression efficiency of these coding schemes. (Article)

1. Motion-Compensated Lifted Haar Wavelet

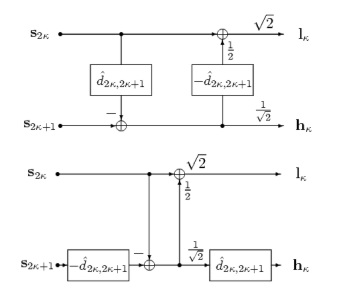
The bottom-left figure shows the equivalent Haar wavelet where the displacement operators are pre- and post-processing operators with respect to the original Haar transform. This scheme is only equivalent to the lifted Haar wavelet (top-left figure), if the displacement operators are invertible.

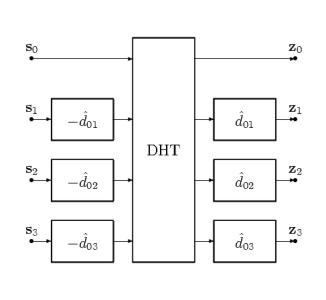
We continue and perform the dyadic decomposition of a GOP with the equivalent Haar wavelet. For that, the displacements of the equivalent Haar blocks have to be added. We assume that the estimated displacements between pairs of frames are additive. As the true displacements are also additive and differ only from the estimated displacement by the displacement error, we conclude that the displacement errors are also additive. The right figure depicts a dyadic decomposition for K=4 pictures based on the equivalent Haar wavelet. The dyadic Haar transform without displacements in the lifting steps is labeled by DHT. The displacements are pre- and post-processing operators with respect to the original dyadic Haar decomposition DHT.

2. Transform Coding Gain

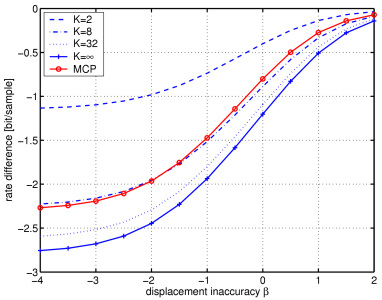The figures depict the rate difference (with respect to optimum intra-frame encoding of the original pictures) over the displacement inaccuracy for a residual noise level of -100 dB (left) and -30 dB (right). We observe that the rate difference starts to saturate for K=32 and that motion-compensated transform coding outperforms motion-compensated prediction (MCP) by at most 0.5 bits per sample.

This work analyzes the efficiency of a compression scheme for video sequences that jointly encodes groups of pictures. Our approach, motion-compensated transform coding, applies a KLT to decorrelate a set of motion-compensated pictures for efficient encoding. The theoretical investigation utilizes a signal model for inaccurate motion compensation and provides a performance comparison to motion-compensated prediction. We discuss the influence of motion accuracy, residual noise, and the correlation of displacement errors dependent on the number of coded pictures. (Article)

1. Motion-Compensated Transform Coding

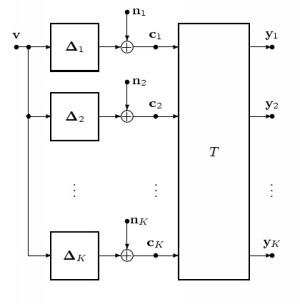
We assume that K pictures are motion-compensated up to a displacement error with given variance and distorted by statistically independent additive white Gaussian noise. We decorrelate the K motion-compensated pictures by the KLT and determine the maximum bit-rate reduction possible by optimum encoding of the transformed signal, compared to optimum intra-frame encoding of the motion-compensated signal.

2. Uncorrelated Displacement Errors

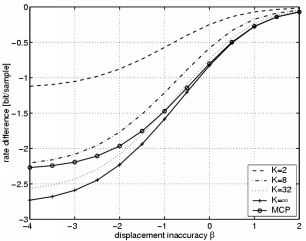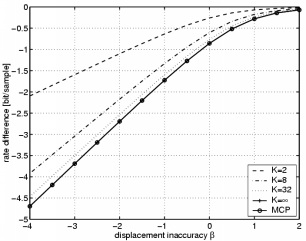
The left figure depicts the noiseless case. For a very large number of pictures K, the performance with uncorrelated displacement errors is identical to that of motion-compensated prediction (MCP). In the presence of residual noise (right figure, RNL = -30 dB), the presented scheme demonstrates an improvement of at most 0.5 bit/sample.

3. Correlated Displacement Errors

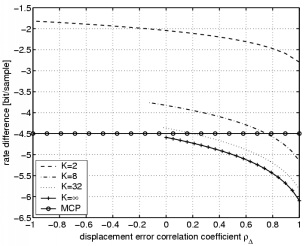For correlated displacement errors, compression efficiency improves for positively correlated displacement errors as shown in the left figure. The performance of motion-compensated transform coding is is only limited by the residual noise. The right figure plots the rate difference over displacement inaccuracy for a group of 2, 8, and 32 pictures at a residual noise level of -30 dB. The displacement error correlation coefficient is 0.5.