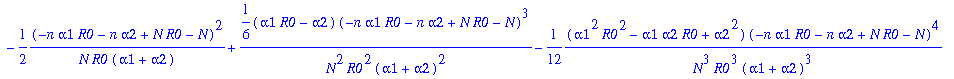
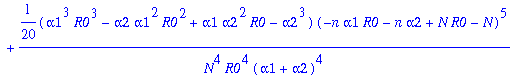
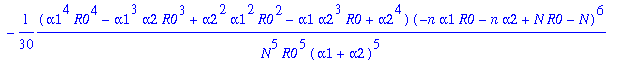
Moments of the stationary distributions of two auxiliary processes for the stochastic logistic model.
This Maple work sheet deals with the Verhulst stochastic logistic model. In particular, it gives approximations of the first three cumulants of the stationary distributions of the two auxiliary processes X0 and X1 in the parameter region where R0>1 as N approaches infinity. The cumulants of X0 are of high importance, since they are actually conjectured to be asymptotic approximations of the corresponding cumulants of the quasi-stationary distribution. The notation used here is described in the appendix of the manuscript "Moment closure and the stochastic logistic model".
momentsX0X1.mws. 2002-03-14.
The assume command is necessary for the simplification of square roots.
> restart;
> assume(alpha1>0,alpha2>0,R0>0,N>0); interface(showassumed=0);
Introduce notation:
>
K:=(R0-1)*N/(alpha1*R0+alpha2):
sigma:=sqrt((alpha1+alpha2)*R0*N)/(alpha1*R0+alpha2):
y1:=(n-K)/sigma:
gamma1:=(1/alpha2)*(((alpha1+alpha2)/alpha1)*log((alpha1*R0+alpha2)/(alpha1+alpha2))-log(R0)):
Define the function h:
> h:=n*log(R0)-(N/alpha1-n)*log(1-alpha1*n/N)-(N/alpha2+n)*log(1+alpha2*n/N):
Taylor expansion of h(n) about n=K! Include 7 terms: The last one includes y1^6 as a factor.
> hKa:=map(simplify,convert(series(h,n=K,7),polynom));
![]()
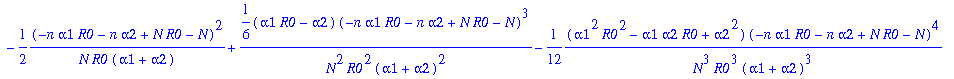
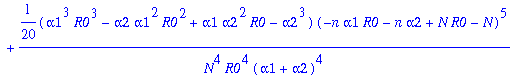
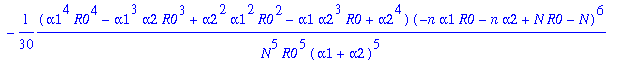
> nops(hKa);
![]()
Show that the sum of the first three terms is equal to
![]() :
:
>
hK1:=simplify(op(1,hKa)+op(2,hKa)+op(3,hKa)):
simplify(hK1/simplify(gamma1*N));
![]()
OK! The linear term (in y1) is lacking. Check that the qudratic term is
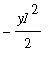 :
:
> simplify(op(4,hKa)/(-y1^2/2));
![]()
OK! Express the remaining terms in terms of y1! Write
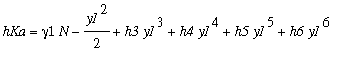 .
.
To determine the coefficients h3, h4, h5, h6!
> for j from 3 to 6 do h||j:=simplify(op(j+2,hKa)/y1^j) end do;
![]()
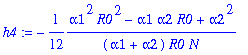
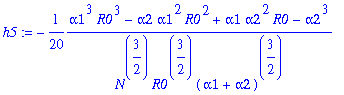
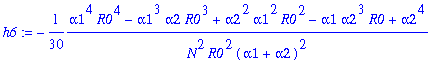
Then expand
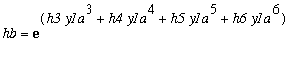 . A temporary name for hb is hba.
. A temporary name for hb is hba.
> hba:=convert(asympt(exp((h3*y1a^3)+(h4*y1a^4)+(h5*y1a^5)+h6*y1a^6),N,3),polynom):
The last term in hba is of the order of
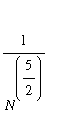 , so I exclude it.
, so I exclude it.
> hb:=hba-op(6,hba);
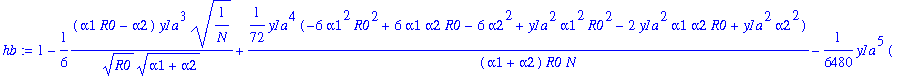
![]()
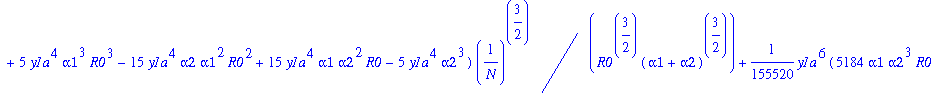
![]()
![]()
![]()
I conclude that
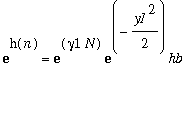 (asymptotically). This can be expressed as
(asymptotically). This can be expressed as
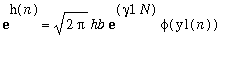 . Define h0 =
. Define h0 =
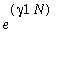 .
.
> h0:=exp(gamma1*N);
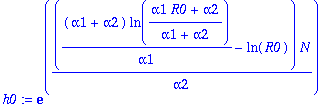
Next define g(n):
> g:=(1/R0)*sqrt(1+alpha2*n/N)/sqrt(1-alpha1*n/N):
Expand g(n) about n=K. Include 5 terms!
> gK:=map(simplify,convert(series(g,n=K,5),polynom));
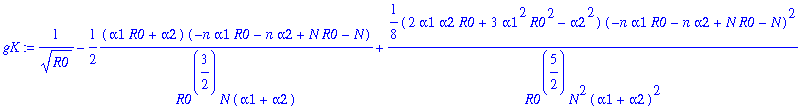
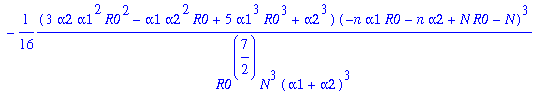
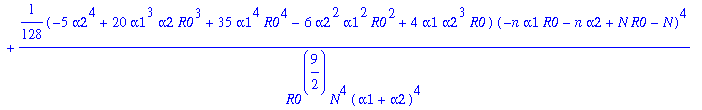
> nops(gK);
![]()
Express this as
![]() . The expression in parentheses is called gb.
. The expression in parentheses is called gb.
> g0:=op(1,gK);
![]()
Determine g1-g4:
> for j from 1 to 4 do g||j:=simplify(op(j+1,gK)/(g0*y1^j)) end do;
![]()
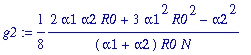
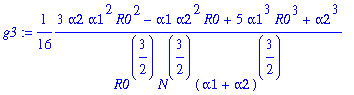
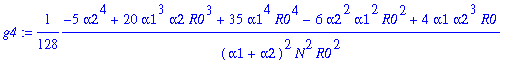
Write g=g0*gb.
> gb:=1+g1*y1a+g2*y1a^2+g3*y1a^3+g4*y1a^4;
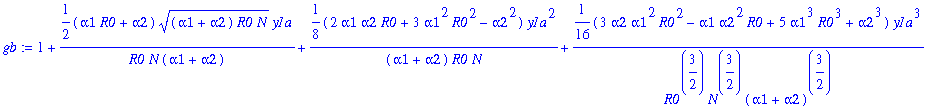
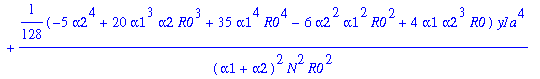
The Stirling expansion "correction". Include two terms in the correction. First define a function called S:
> S:=N->1+1/(12*N)+1/(288*N^2);
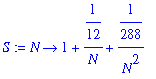
> n1:=N/alpha1: n2:=N/alpha2: n3:=n1-n: n4:=n2+n:
>
s0a:=S(n1)*S(n2);
s1:=1/S(n3);
s2:=1/S(n4);
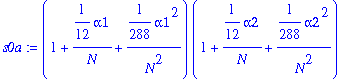
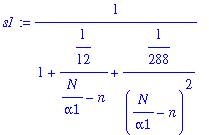
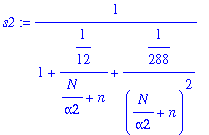
> s0:=map(factor,convert(asympt(s0a,N,3),polynom));
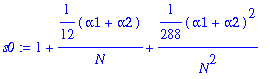
Expand s1 as Taylor series about n=K. Include terms up to order
![]() .
.
> s1a:=map(simplify,convert(series(s1,n=K,3),polynom)):
There are three terms in this series expansion. Asymptotic approximation of the first one:
> s1a1:=map(simplify,convert(asympt(op(1,s1a),N,3),polynom));
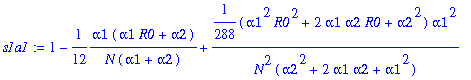
Asymptotic approximation of the second term divided by y1:
> s1a2:=factor(convert(asympt(op(2,s1a)/y1,N,5),polynom));
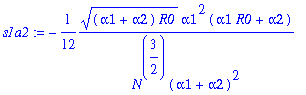
The third term divided by
![]() is approximated as follows:
is approximated as follows:
> s1a3:=factor(convert(asympt(op(3,s1a)/y1^2,N,7),polynom));
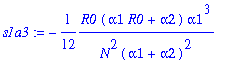
The resulting asymptotic approximation of s1(n) can be written as follows:
> s1b:=map(simplify,map(factor,s1a1+s1a2*y1a+s1a3*y1a^2));
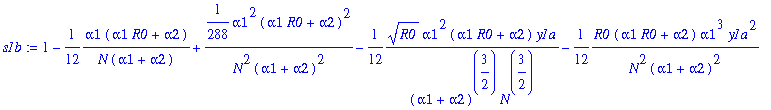
A similar treatment of s2(n):
> s2a:=map(simplify,convert(series(s2,n=K,3),polynom)):
> s2a1:=map(factor,convert(asympt(op(1,s2a),N,3),polynom));
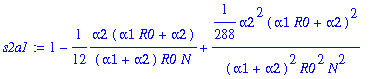
> s2a2:=factor(convert(asympt(op(2,s2a)/y1,N,5),polynom));
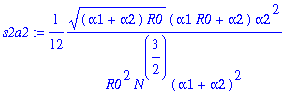
> s2a3:=factor(convert(asympt(op(3,s2a)/y1^2,N,7),polynom));
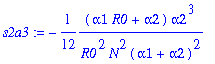
> s2b:=map(simplify,s2a1+s2a2*y1a+s2a3*y1a^2);
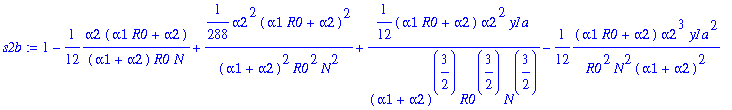
An asymptotic approximation of the product of s1b and s2b:
> sba:=map(factor,convert(asympt(s1b*s2b,N,3),polynom)):
> nops(%);
![]()
> sb:=map(simplify,sba-op(5,sba));
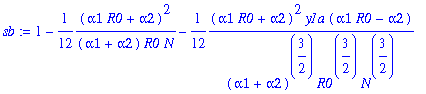
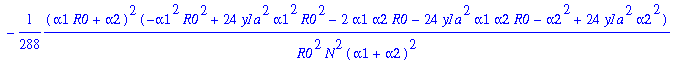
Finally, work with f(n)=mu1/mun = f0a*fa(n), where f0=1+alpha2/N, and fa=1/(n*(1+alpha2*n/N)).
> f0a:=1+alpha2/N;
![]()
> fa:=1/(n*(1+alpha2*n/N));
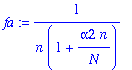
Expand about n=K:
> faK:=convert(map(simplify,series(fa,n=K,5)),polynom):
> nops(%);
![]()
Write faK=f0b*fb(n), where f0b=1+f1*y1 + f2*y1^2 + f3*y1^3 +f4*y1^4. Determine f0b and f1-f4:
> f0b:=op(1,faK);
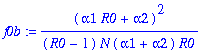
> for j from 1 to 4 do f||j:=simplify(op(j+1,faK)/(f0b*y1^j)) end do;
![]()
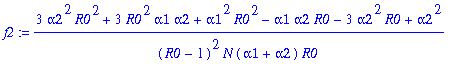
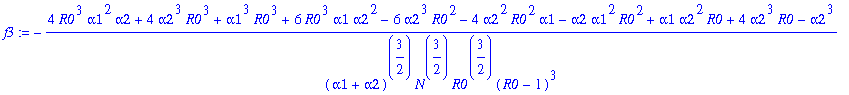
![]()
![]()
Write f(n)= f0*fb(n), with f0=f0a*f0b.
> fb:=1+f1*y1a+f2*y1a^2+f3*y1a^3+f4*y1a^4;
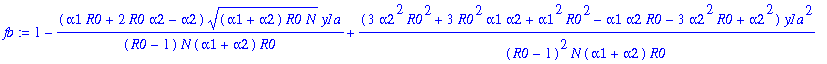
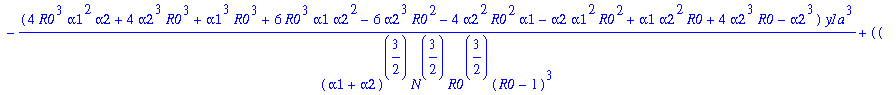
![]()
![]()
> f0:=asympt(f0a*f0b,N);
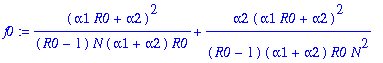
Continue with pi(n)!!!
> pi0:=exp(gamma1*N)*map(simplify,convert(asympt(s0*f0*g0,N,3),polynom));
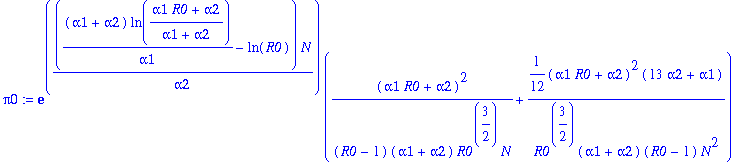
> piba:=convert(asympt(fb*gb*hb*sb,N,3),polynom):
> nops(piba);
![]()
The response to the following command is long. I use a colon to prevent it being shown.
> pib:=sum(op('j',piba),'j'=1..5):
For curiosity, I gave the command map(simplify,pib). The result was two and one half pages long! When I saw this first, I was discouraged. It did not seem likely, or even possible, that the end result could be as simple as I was guessing, when intermediate expressions were so complicated.
Write pib=k0+k1*y1+...+k12*y1^12. The following command determines the coefficients k0, k1, k2,...,k12:
> for j from 0 to 12 do k||j:=map(simplify,coeff(pib,y1a,j)) end do;
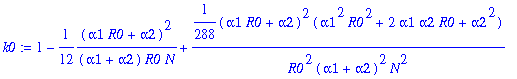
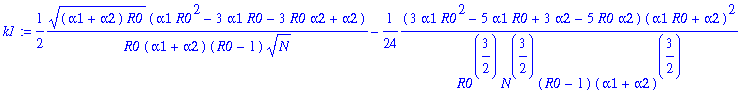
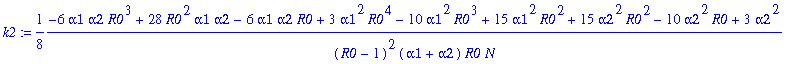
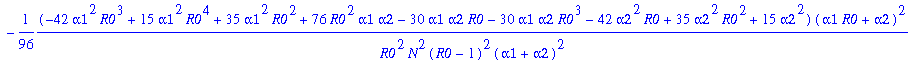
![]()
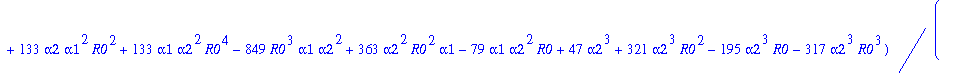
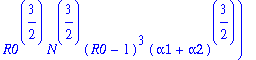
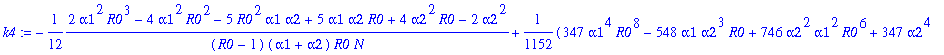
![]()
![]()
![]()
![]()
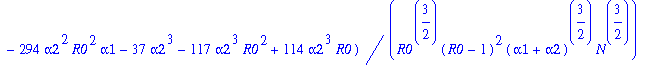
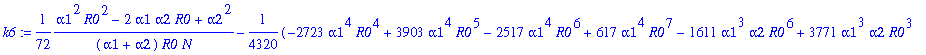
![]()
![]()
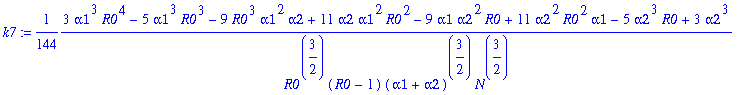
![]()
![]()
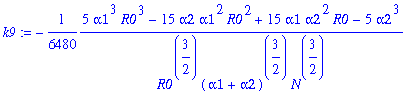
![]()
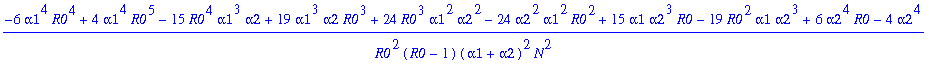
![]()
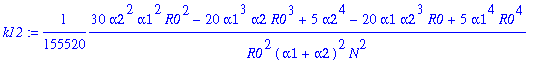
Determine the stationary distribution p0(n) as p0(n)=pi(n)/sum(pi(n)).
I have p0(n)=pib*phi(y1(n))/p0d, (the letter d indicates denominator), where
> p0d:=map(simplify,asympt(k0+k2+3*k4+15*k6+105*k8+945*k10+945*11*k12,N));
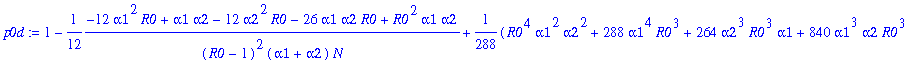
![]()
![]()
Now I can determine the moments of the stationary distribution of X0!!
> EX0:=map(factor,map(simplify,convert(asympt(K+sigma*(k1+3*k3+15*k5+105*k7+945*k9)/p0d,N,2),polynom)));
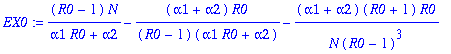
> VX0a:=map(simplify,convert(asympt(sigma^2*(k0+3*k2+15*k4+105*k6+945*k8+10395*k10+135135*k12)/p0d-(EX0-K)^2,N,2),polynom));
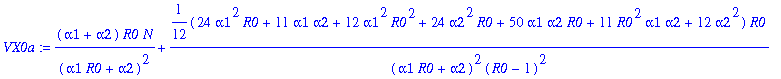
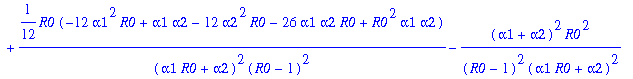
> nops(%);
![]()
> VX0:=map(factor,op(1,VX0a)+simplify(sum(op('j',VX0a),'j'=2..4)));
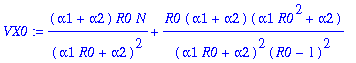
> simplify((sigma^2/K)*((R0+1)/(R0-1)-sigma^2/K));
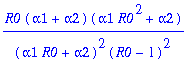
Agrees with what I have found before !!!! The third cumulant:
> kappa3a:=factor(simplify(convert(asympt(sigma^3*(3*k1+15*k3+105*k5+945*k7+110395*k9)/p0d - 3*VX0*(EX0-K)-(EX0-K)^3,N,1),polynom)));
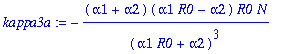
Agrees with what I have found before!!!
Now look at the moments of X1! The only difference is that the factor f(n) shold not be included.
> rhoba:=convert(asympt(gb*hb*sb,N,3),polynom):
> rhob:=map(simplify,sum(op('j',rhoba),'j'=1..5));
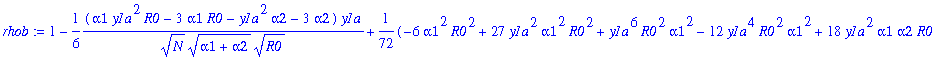
![]()
![]()
![]()
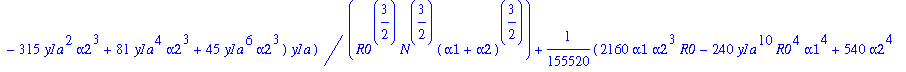
![]()
![]()
![]()
![]()
![]()
> for j from 0 to 12 do kk||j:=map(simplify,coeff(rhob,y1a,j)) end do;
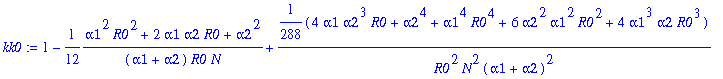
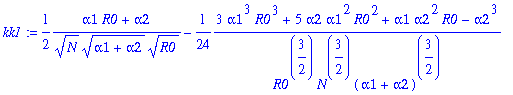
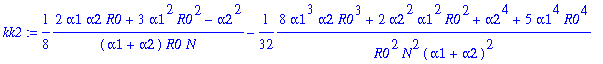
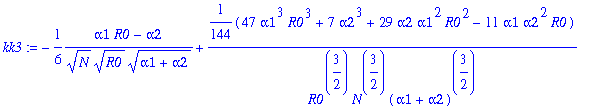
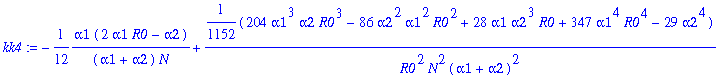
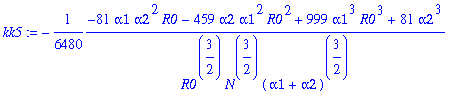
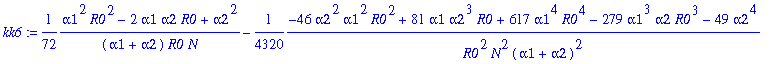
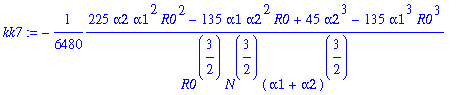
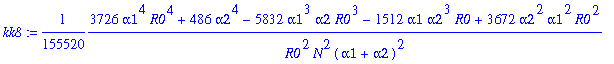
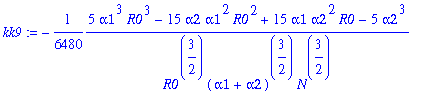
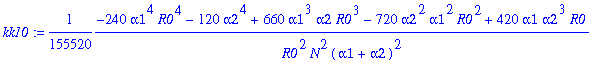
![]()
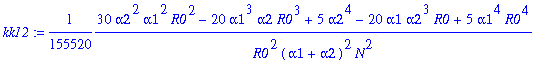
> p1d:=map(simplify,asympt(kk0+kk2+3*kk4+15*kk6+105*kk8+945*kk10+945*11*kk12,N));
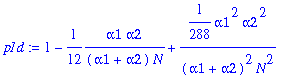
> EX1:=map(factor,map(simplify,convert(asympt(K+sigma*(kk1+3*kk3+15*kk5+105*kk7+945*kk9)/p1d,N,2),polynom)));
![]()
> VX1a:=map(simplify,convert(asympt(sigma^2*(kk0+3*kk2+15*kk4+105*kk6+945*kk8+10395*kk10+135135*kk12)/p1d-(EX1-K)^2,N,2),polynom));
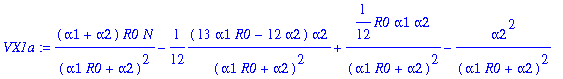
> VX1:=map(factor,op(1,VX1a)+simplify(sum(op('j',VX1a),'j'=2..4)));
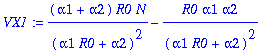
> kappa3:=factor(simplify(convert(asympt(sigma^3*(3*kk1+15*kk3+105*kk5+945*kk7+110395*kk9)/p1d - 3*VX1*(EX1-K)-(EX1-K)^3,N,1),polynom)));
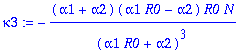
>