phaseportnormal2.mws

Plot phase portrait for moment closure equations for Verhulst logistic model, assuming normal distribution.

This Maple work sheet uses Maple8,  and the new package LinearAlgebra.  Date 030402.

>	restart; with(DEtools,DEplot); with(plots,display); with(LinearAlgebra,Eigenvectors); with(VectorCalculus,Jacobian); XP:=Vector(2);

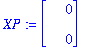
In the original Verhulst model, take alpha1=alpha2=1, R0=4, N=100. Then a1=3/5, f1=5/3, f2=3/5. Take r/K=1 (by rescaling time). Put kappa1=X[1], kappa2=X[2].

The equations are given by the procedure G:

>	G:=proc(N,t,X,XP)    XP[1]:=(60-X[1])*X[1]-X[2];    XP[2]:=(100-0.6*X[1])*X[1]+119.4*X[2]-4*X[1]*X[2];    end;

Run G to determine XP:

>	G(2,t,X,XP):

We determine the isoclines where the derivatives are equal to zero:

>	isocline1:=solve(XP[1],X[2]); isocline2:=solve(XP[2],X[2]);

Plot the isoclines:

>	plot({isocline1,isocline2},X[1]=-10..100,y=-100..1000,discont=true);

>	expand(subs(X[2]=isocline1,XP[2]));

>	plot(%,X[1]=-10..70);

There are three critical points. Solve for them:

>	critp:=solve({XP[1],XP[2]},{X[1],X[2]});

I use P1, P2, P3 to denote the three critical points. They are numbered from the left.

CHECK the numbering here!

>	P1prel:=critp[1]; P2prel:=critp[2]; P3prel:=critp[3];

CHECK the ordering here!

>	P1:=[rhs(P1prel[1]),rhs(P1prel[2])]; P2:=[rhs(P2prel[1]),rhs(P2prel[2])]; P3:=[rhs(P3prel[1]),rhs(P3prel[2])];

Now determine the Jacobian of the right-hand sides of the given system of equations:

>	J:=Jacobian(XP,[X[1],X[2]]);

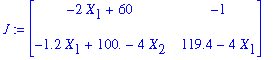
Determine the jacobian in each of the critical points:

>	J1:=subs(P1prel,J);

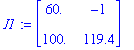
>	J2:=subs(P2prel,J);

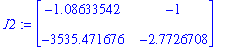
>	J3:=subs(P3prel,J);

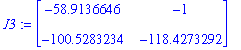
The eigenvalues and eigenvectors of these three matrices:

>	eg1:=Eigenvectors(J1,output=list);

>	eg2:=Eigenvectors(J2,output=list);

>	eg3:=Eigenvectors(J3,output=list);

Notice that P1 is an unstable node, P2 is a saddle point, P3 is a stable node. Furthermore,

CHECK the numbering here!

eg1[1] : slow manifold,     eg1[2]: fast manifold of unstable node P0. Both manifolds have negative slopes.

eg2[1]: unstable manifold, eg2[2]: stable manifold of saddle point P1.

eg3[1]: slow manifold,      eg3[2]: fast manifold of stable node P2.

A Maple procedure for determining initial values on each manifold near each critical point...

Think of it as transforming eg-to-init (eg2init):

>

eg2init:=proc(P,eg,d)  local u,lu,v,k;  u:=eg[3]; # This is an eigenvector.  lu:=sqrt(u[1]^2+u[2]^2); # This is the length of the eigenvector u.  v:=d*u/lu; # This is a vector of length d in the direction of u.  [seq([x(0)=P[1]+(-1)^k*v[1],y(0)=P[2]+(-1)^k*v[2]],k=1..2)];  #These are two initial values near P in the direction of the eigenvector. end proc:

CHECK the numbering here!

>	init2unstable:=eg2init(P2,eg2[1],10); init2stable:=eg2init(P2,eg2[2],10); init3fast:=eg2init(P3,eg3[2],10);

Plot orbits on the unstable manifold at P2:

>	plot2unstable:=DEplot(G,[x(t),y(t)],t=0..0.2,number=2,init2unstable,x=-10..100,y=-100..1000,arrows=none,stepsize=0.01,linecolor=red,thickness=4): plot2unstable;

Plot orbits on the stable manifold at P2:

>	plot2stable:=DEplot(G,[x(t),y(t)],t=-0.2..0,number=2,init2stable,x=-10..100,y=-100..1000,arrows=none,stepsize=0.01,linecolor=red,thickness=4): plot2stable;

Plot orbits on the fast manifold at P3:

>	plot3fast:=DEplot(G,[x(t),y(t)],t=-0.04..0,number=2,init3fast,x=-10..100,y=-100..1000,arrows=none,linecolor=red,stepsize=0.01,thickness=4): plot3fast;

Plot one orbit on the slow manifold at P3:

>	plot3slow:=DEplot(G,[x(t),y(t)],t=0..0.1,number=2,{[x(0)=500,y(0)=20]},x=-10..100,y=-100..1000,stepsize=0.002,arrows=none,linecolor=red,thickness=4): plot3slow;

NOTE:  The arrows on the final phase portrait become less pronounced if the commend "color=red" below is replaced by "color=yellow".   

Plot a direction field:

>	plotarrows:=DEplot(G,[x(t),y(t)],t=0..0.01,number=2,{[x(0)=60,y(0)=32]},x=-10..100,y=-100..1000,stepsize=0.01,color=red,linecolor=red): plotarrows;

Plot three additional orbits:

>	init1:=[x(0)=10,y(0)=0]; plot1:=DEplot(G,[x(t),y(t)],t=0..0.1,number=2,[init1],x=-10..100,y=-100..1000,stepsize=0.01,arrows=none,linecolor=red,thickness=4): plot1;

>	init2:=[x(0)=50,y(0)=1000]; plot2:=DEplot(G,[x(t),y(t)],t=0..0.1,number=2,[init2],x=-10..100,y=-100..1000,stepsize=0.01,arrows=none,linecolor=red,thickness=4): plot2;

>	init3:=[x(0)=100,y(0)=1000]; plot3:=DEplot(G,[x(t),y(t)],t=0..0.1,number=2,[init3],x=-10..100,y=-100..1000,stepsize=0.002,arrows=none,linecolor=red,thickness=4): plot3;

Plot all these orbits in one figure:

>	display({plot2stable,plot2unstable,plot3fast,plot3slow,plotarrows,plot1,plot2,plot3},labels=[Mean,Variance],title=Normal_Assumption);

>