Determine the critical points of the first three moment closure equations for the Verhulst model, and their stabilities, under assumption of Poisson distribution!

>

restart;

>	with(LinearAlgebra,Eigenvalues); with(VectorCalculus,Jacobian);

The differential equations for the first three cumulants:

>	eq1:=(a1*N-kappa1)*kappa1-kappa2;

>	eq2:=(f1*a1*N-f2*kappa1)*kappa1+(2*a1*N-f2)*kappa2-4*kappa1*kappa2-2*kappa3;

>	eq3prel:=(a1*N-kappa1)*kappa1-6*f2*kappa1*kappa2-6*kappa1*kappa3+(3*f1*a1*N-1)*kappa2-6*kappa2^2+3*(a1*N-f2)*kappa3-3*kappa4;

For the Poisson distribution we have kappa4=kappa1:

>	eq3:=subs(kappa4=kappa1,eq3prel);

Solve the first equation for kappa2. This gives kappa2 as a function of kappa1.

>	kap2:=solve(eq1,kappa2);

Substitute this value of kappa2 into the second equation.

>	eq2a:=subs(kappa2=kap2,eq2);

Solve this equation for kappa3. This gives kappa3 as a function of kappa1.

>	kap3:=solve(eq2a,kappa3);

Insert the values of kappa2 and kappa3 into eq3 divided by minus 3. This gives an expression in kappa1.

>	eq3a:=-map(simplify,collect(subs(kappa2=kap2,kappa3=kap3,eq3),kappa1))/3;

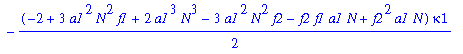
The problem now is to solve this forth-degree equation in kappa1. (Some minor (cosmetic) simplification can be achieved by introducing K and sigma^2.)  One root is equal to 0. The corresponding values for kappa2 and kappa3 are also 0:

>	kap20:=subs(kappa1=0,kap2);

>	kap30:=subs(kappa1=0,kap3);

The remaining 3 roots of eq3a satisfy the following third-degree equation:

>	eq3b:=collect(eq3a/kappa1,kappa1);

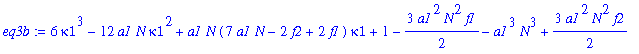
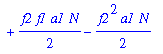
Look for asymptotic approximation! Put kappa1 = AN + B + C/N .

>	eq3c:=subs(kappa1=A*N+B+C/N,eq3b);

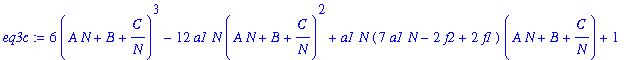
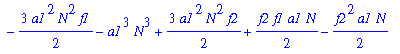
Form 3 equations (for A,B,C) by putting the coefficients of N^3, N^2, N^1 equal to zero.

>	eqA:=coeff(eq3c,N,3);

>	eqB:=coeff(eq3c,N,2);

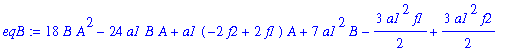
>	eqC:=coeff(eq3c,N,1);

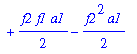
>	AA:=solve(eqA,A);

>

evalf(%);

The A values of the remaining 3 critical points are given by AA[1]-AA[3]. I expect AA[2], AA[3] to correspond to spurious solutions.  

Determine asymptotic approx of the 3 coordinates of each of the remaining 3 critical points:

>	eqB1:=simplify(subs(A=AA[1],eqB));

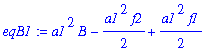
>	BB[1]:=solve(eqB1,B);

>	eqC1:=simplify(subs(A=AA[1],B=BB[1],eqC));

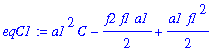
>	CC[1]:=solve(eqC1,C);

An asymptotic approximation for the first non-zero solution for kappa1 has thus been found. It is

AA[1]*N + BB[1] + CC[1]/N. Use it to derive asymptotic approximations of kappa2 and kappa3, using kap2 and kap3.  

Write kappa2 sim DD[1]*N+EE[1]  and  kapp3 sim FF[1]*N.

>

kap2;

>	kap21:=simplify(convert(asympt(subs(kappa1=AA[1]*N+BB[1]+CC[1]/N,kap2),N,2),polynom));

>	DD[1]:=coeff(kap21,N,1);

>	EE[1]:=factor(simplify(coeff(kap21,N,0)));

>	kap31:=simplify(map(simplify,convert(asympt(subs(kappa1=AA[1]*N+BB[1]+CC[1]/N,kap3),N,2),polynom)));

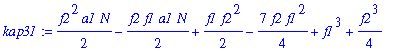
>	FF[1]:=factor(coeff(kap31,N,1));

Now proceed to find approximations of the remaining 2 critical points, with subscripts 2 and 3. First I work on A,B,C.

>	eqB2:=simplify(subs(A=AA[2],eqB));

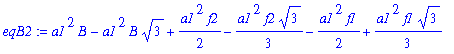
>	BB[2]:=factor(solve(eqB2,B));

>	eqC2:=simplify(subs(A=AA[2],B=BB[2],eqC));

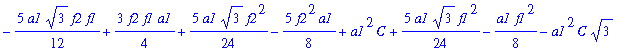
>	CC[2]:=factor(solve(eqC2,C));

>	kap22:=map(factor,collect(simplify(convert(asympt(subs(kappa1=AA[2]*N+BB[2]+CC[2]/N,kap2),N,1),polynom)),N));

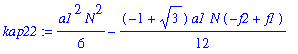
>	DD[2]:=coeff(kap22,N,2);

>	EE[2]:=coeff(kap22,N,1);

So kappa2 is sim DD[2]*N^2 + EE[2]*N

>	kap32:=simplify(convert(asympt(subs(kappa1=AA[2]*N+BB[2]+CC[2]/N,kap3),N,1),polynom));

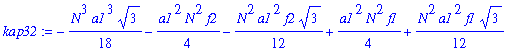
>	FF[2]:=coeff(kap32,N,3);

And kappa3 = FF[2]*N^3.  Now work on the last of the critical points!

>	eqB3:=simplify(subs(A=AA[3],eqB));

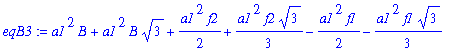
>	BB[3]:=factor(solve(eqB3,B));

>	eqC3:=simplify(subs(A=AA[3],B=BB[3],eqC));

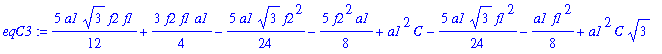
>	CC[3]:=factor(solve(eqC3,C));

>	kap23:=simplify(convert(asympt(subs(kappa1=AA[3]*N+BB[3]+CC[3]/N,kap2),N,1),polynom));

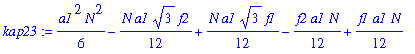
>	DD[3]:=coeff(kap23,N,2);

>	EE[3]:=factor(simplify(coeff(kap23,N,1)));

>	kap33:=simplify(convert(asympt(subs(kappa1=AA[3]*N+BB[3]+CC[3]/N,kap3),N,1),polynom));

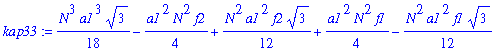
>	FF[3]:=coeff(kap33,N,3);

So kappa2 sim DD[3]*N^2 + EE[3]*N, and kappa3 sim FF[3]*N^3.

I have now derived asymptotic approximatons of the first three cumulants at each of the 4 critical points.

I would also like to study the local stability of the 4 critical points.  I do this by evaluating the eigenvalues of the jacobian matrices evaluated at each of the four critical points...

>	F:=[eq1,eq2,eq3];

>	J:=Jacobian(F,[kappa1,kappa2,kappa3]);

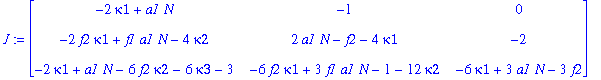
Determine the Jacobian in each of the four critical points:

>	J0:=subs(kappa1=0,kappa2=0,kappa3=0,J);

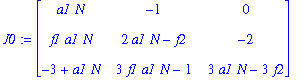
>	J1:=subs(kappa1=AA[1]*N+BB[1]+CC[1]/N,kappa2=DD[1]*N+EE[1],kappa3=FF[1]*N,J):

>	J2:=subs(kappa1=AA[2]*N+BB[2]+CC[2]/N,kappa2=DD[2]*N^2+EE[2]*N,kappa3=FF[2]*N^3,J):

>	J3:=subs(kappa1=AA[3]*N+BB[3]+CC[3]/N,kappa2=DD[3]*N^2+EE[3]*N,kappa3=FF[3]*N^3,J):

Determine the eigenvalues of the matrix J0. Expect instability...

>	a1:='a1': eg0:=Eigenvalues(J0):

Asymptotic approximations of the eigenvalues of J0:

>	a1:='a1': eg01a:=convert(asympt(eg0[1],N,3),polynom):

>	assume(a1>0); eg01b:=simplify(evalc(eg01a));

>	a1:='a1': eg02a:=convert(asympt(eg0[2],N,3),polynom):

>	assume(a1>0); eg02b:=simplify(evalc(eg02a));

>	a1:='a1': eg03a:=convert(asympt(eg0[3],N,3),polynom):

>	assume(a1>0); eg03b:=simplify(evalc(eg03a));

>

a1:='a1';

The three eigenvalues are asymptotically K+f1, 2K+5f1-f2, 3K-6f1-3f2. All of them positive. So the origin (or rather the critical point whose coordinates are exponentially small) is unstable.

Next consider the eigenvalues of the matrix J1.

>	a1:='a1': eg1:=Eigenvalues(J1):

Asymptotic approximations of the eigenvalues:

>	a1:='a1': eg11a:=evalc(convert(asympt(eg1[1],N,4),polynom)):

>	assume(a1>0); eg11b:=simplify(eg11a);

>	a1:='a1': eg12a:=evalc(convert(asympt(eg1[2],N,3),polynom)):

>	assume(a1>0); eg12b:=simplify(eg12a);

>	a1:='a1': eg13a:=evalc(convert(asympt(eg1[3],N,3),polynom)):

>	assume(a1>0); eg13b:=simplify(eg13a);

>

a1:='a1';

The eigenvalues are, asymptotically, -K+2f1-f2, -3K-3f1-6f2, -2K+7f1-3f2. Hence the critical point P1 is as stable.

Now look at the eigenvalues of J2. The computations are demanding. Simplification can be achieved by modifying J2, replacing each of its elements by the first two terms in its asymptotic approximation as N approaches infinity. The modified matrix is denoted J2a.

>

J2a:=J2:

>	J2a[1,1]:=map(factor,convert(asympt(J2[1,1],N,1),polynom));

>

J2a[1,2];

>

J2a[1,3];

>	J2a[2,1]:=map(factor,convert(asympt(J2[2,1],N,0),polynom));

>	J2a[2,2]:=map(factor,convert(asympt(J2[2,2],N,1),polynom));

>

J2a[2,3];

>	J2a[3,1]:=convert(asympt(J2[3,1],N,-1),polynom);

>	J2a[3,2]:=map(factor,convert(asympt(J2[3,2],N,0),polynom));

>	J2a[3,3]:=map(factor,convert(asympt(J2[3,3],N,1),polynom));

The eigenvalues of J2a:

>	a1:='a1': eg2:=Eigenvalues(J2a):

>	a1:='a1': eg21a:=convert(asympt(eg2[1],N,3),polynom):

>	assume(a1>0); eg21b:=evalf(simplify(evalc(eg21a)));

>	a1:='a1': eg22a:=convert(asympt(eg2[2],N,3),polynom):

>	assume(a1>0): eg22b:=evalf(simplify(evalc(eg22a)));

>	a1:='a1': eg23a:=convert(asympt(eg2[3],N,3),polynom):

>	assume(a1>0); eg23b:=evalf(simplify(evalc(eg23a)));

>

a1:='a1';

So the eigenvalues of J2 are asymptotically equal to  K,  -K,  -3.46K.  Unstable critical point!  

Now look at the eigenvalues of J3. Approximate J3 by the modified matrix J3a.

>

J3a:=J3:

>	J3a[1,1]:=map(factor,convert(asympt(J3[1,1],N,1),polynom));

>

J3a[1,2];

>

J3a[1,3];

>	J3a[2,1]:=map(factor,convert(asympt(J3[2,1],N,0),polynom));

>	J3a[2,2]:=map(factor,convert(asympt(J3[2,2],N,1),polynom));

>

J3a[2,3];

>	J3a[3,1]:=convert(asympt(J3[3,1],N,-1),polynom);

>	J3a[3,2]:=map(factor,convert(asympt(J3[3,2],N,0),polynom));

>	J3a[3,3]:=map(factor,convert(asympt(J3[3,3],N,1),polynom));

The eigenvalues of J3a:

>	a1:='a1': eg3:=Eigenvalues(J3a):

Asymptotic approximations of the eigenvalues:

>	a1:='a1': eg31a:=convert(asympt(eg3[1],N,3),polynom):

>	assume(a1>0); eg31b:=evalf(simplify(evalc(eg31a)));

>	a1:='a1': eg32a:=convert(asympt(eg3[2],N,3),polynom):

>	assume(a1>0); eg32b:=evalf(simplify(evalc(eg32a)));

>	a1:='a1': eg33a:=convert(asympt(eg3[3],N,3),polynom):

>	assume(a1>0); eg33b:=evalf(simplify(evalc(eg33a)));

>

The eigenvalues of J3 are asymptotically 3.46K, K, -K.  Thus P3 is unstable.