lognormal2.mws  030224

Determine the critical points of the first two moment closure equations, and their stabilities, under assumption of log-normality!

>

restart;

>	with(VectorCalculus,Jacobian); with(LinearAlgebra,Eigenvalues);

The rhss of the differential equations for the first two cumulants are eq1 and eq2prel. I reserve the name eq2 for the rhs of the second moment closure equation.

>	eq1:=(a1*N-kappa1)*kappa1-kappa2;

>	eq2prel:=(f1*a1*N-f2*kappa1)*kappa1+(2*a1*N-f2)*kappa2-4*kappa1*kappa2-2*kappa3;

The log-normality assumption means that kappa3=3kappa2^2/kappa1 + kappa2^3/kappa1^3:

>	eq2:=subs(kappa3=3*kappa2^2/kappa1+kappa2^3/kappa1^3,eq2prel);

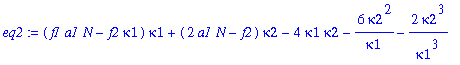
Solve the first equation for kappa2:

>	kap2:=solve(eq1,kappa2);

Substitute this value of kappa2 into the second equation.

>	eq2a:=subs(kappa2=kap2,eq2);

>	x:=solve(eq2a,kappa1);

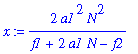
There is ONLY ONE  critical point, with this kappa1-value. The corresponding kappa2-coordinate is:

>	y:=simplify(subs(kappa1=x,kap2));

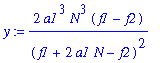
Asymptotic approximations of the coordinates of the critical point:

>	xasymp:=map(simplify,convert(asympt(x,N,2),polynom));

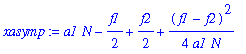
>	yasymp:=map(simplify,convert(asympt(y,N,4),polynom));

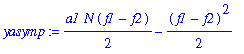
The stability of the critical point:

>	F:=[eq1,eq2];

>	J:=Jacobian(F,[kappa1,kappa2]);

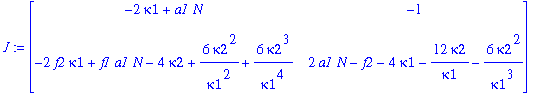
Determine the Jacobian at the critical point:

>	J1:=subs(kappa1=x,kappa2=y,J);

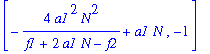
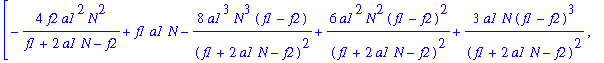
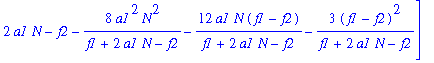
The eigenvalues are:

>	eg1:=Eigenvalues(J1);

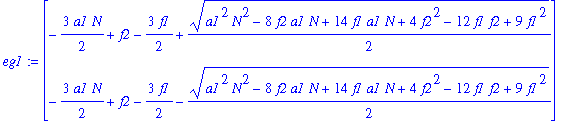
Asymptotic approximations of the two eigenvalues are:

>	assume(a1>0);

>	simplify(convert(asympt(eg1[1],N,1),polynom));

>	simplify(convert(asympt(eg1[2],N,1),polynom));

>

So both of the eigenvalues of the critical point are negative. Hence it is a stable node.