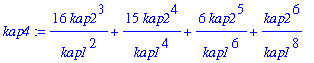kappa34.mws 030128
Determine cumulants for 1) Poisson distribution, 2) Binomial distribution, 3) Log-normal distribution
| > | restart; |
1) Begin with Poisson distribution. Determine the first 4 moments about zero.
| > | sum(lambda^k*exp(-lambda)/k!,k=0..infinity); |
| > | alpha1:=sum(k*lambda^k*exp(-lambda)/k!,k=0..infinity); |
| > | alpha2:=sum(k^2*lambda^k*exp(-lambda)/k!,k=0..infinity); |
| > | alpha3:=sum(k^3*lambda^k*exp(-lambda)/k!,k=0..infinity); |
| > | alpha4:=sum(k^4*lambda^k*exp(-lambda)/k!,k=0..infinity); |
![]()
![]()
![]()
![]()
![]()
The cumulants are determined from the moments:
| > | kappa1:=alpha1; kappa2:=expand(alpha2-alpha1^2); kappa3:=expand(alpha3-3*alpha2*alpha1+2*alpha1^3); kappa4:=expand(alpha4-4*alpha3*alpha1-3*alpha2^2+12*alpha2*alpha1^2-6*alpha1^4); |
![]()
![]()
![]()
![]()
2) Now turn to a binomially distributed r.v.:
| > | restart; |
The first four moments are determined as functions of the parameters N and p:
| > | simplify(sum(binomial(N,k)*p^k*(1-p)^(N-k),k=0..N),symbolic); |
| > | alpha1:=simplify(sum(k*binomial(N,k)*p^k*(1-p)^(N-k),k=0..N),symbolic); |
| > | alpha2:=map(simplify,sum(k^2*binomial(N,k)*p^k*(1-p)^(N-k),k=0..N),symbolic); |
| > | alpha3:=map(simplify,sum(k^3*binomial(N,k)*p^k*(1-p)^(N-k),k=0..N),symbolic); |
| > | alpha4:=map(simplify,sum(k^4*binomial(N,k)*p^k*(1-p)^(N-k),k=0..N),symbolic); |
![]()
![]()
![]()
![]()
![]()
The cumulants are determined from the moments:
| > | kappa1:=alpha1; |
| > | kappa2:=expand(alpha2-alpha1^2); |
| > | kappa3:=expand(alpha3-3*alpha2*alpha1+2*alpha1^3); |
| > | kappa4:=expand(alpha4-4*alpha3*alpha1-3*alpha2^2+12*alpha2*alpha1^2-6*alpha1^4); |
![]()
![]()
![]()
![]()
I wish to express kappa3 and kappa4 in terms of kappa1 and kappa2. Solve the first two equations above for N and p in terms of kappa1 and kappa2: Get kappa1*(1-p)=kappa2; hence p=1-kappa2/kappa1.
| > | simplify(subs(N=kap1/(1-kap2/kap1),p=1-kap2/kap1,kappa3)); |
![]()
| > | simplify(subs(N=kap1/(1-kap2/kap1),p=1-kap2/kap1,kappa4)); |
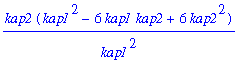
3) Log-normal distribution: Y=ln(X/x0) is N(mu,sigma). I have X=x0*exp(Y). Hence
![]() =
=
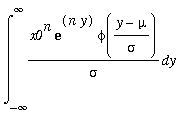 , where
, where
![]() is the normal density. By completing the square and integrating, I get
is the normal density. By completing the square and integrating, I get
![]() =
=
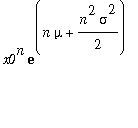 .
.
| > | restart; |
The moments are determined from mu and sigma as folloes:
| > | alpha:=n->x0^n*exp(n*mu+n^2*sigma^2/2); |
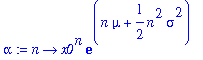
The first four cumulants:
| > | kappa1:=alpha(1); |
| > | kappa2:=simplify(alpha(2)-alpha(1)^2); |
| > | kappa3:=simplify(alpha(3)-3*alpha(1)*alpha(2)+2*alpha(1)^3); |
| > | kappa4:=simplify(alpha(4)-3*alpha(2)^2-4*alpha(1)*alpha(3)+12*alpha(1)^2*alpha(2)-6*alpha(1)^4); |
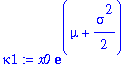
![]()
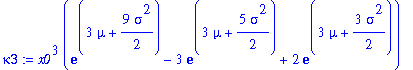
![]()
Note that kappa_k contains the factor kappa_1^k. I simplify the expressions for the cumulants:
| > | expand(simplify(kappa2/kappa1^2,power)); |
| > | simplify(expand(simplify(kappa3/kappa1^3,power)),power); |
| > | simplify(expand(simplify(kappa4/kappa1^4,power)),power); |
![]()
![]()
![]()
I wish to express the cumulants kappa3 and kappa4 in terms of kappa1 and kappa2.
The first of these expressions is solved for exp(sigma^2) in terms of kappa2 and kappa1. I get exp(sigma^2)=1+kappa2/kappa1^2. Use the notation kap_k for kappa_k, and
| > | esig:=1+kap2/kap1^2; |
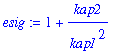
| > | kap3:=expand(kap1^3*(esig^3-3*esig+2)); |
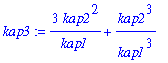
| > | kap4:=expand(kap1^4*(esig^6-4*esig^3-3*esig^2+12*esig-6)); |