general2.mws

general2.mws  030214

Determine the critical points of the first two moment closure equations, and their stabilities, under assumption that the third cumulant is of order N.

This Maple worksheet uses Maple 8, and the "new" package LinearAlgebra. 030226.

>    restart;

>    with(VectorCalculus,Jacobian);
with(LinearAlgebra,Eigenvalues);

[Jacobian]

[Eigenvalues]

>    eq1:=(a1*N-kappa1)*kappa1-kappa2;

eq1 := (a1*N-kappa1)*kappa1-kappa2

>    eq2prel:=(f1*a1*N-f2*kappa1)*kappa1+(2*a1*N-f2)*kappa2-4*kappa1*kappa2-2*kappa3;

eq2prel := (f1*a1*N-f2*kappa1)*kappa1+(2*a1*N-f2)*kappa2-4*kappa1*kappa2-2*kappa3

The assumption is that kappa3 = a3*N:

>    eq2:=subs(kappa3=a3*N,eq2prel);

eq2 := (f1*a1*N-f2*kappa1)*kappa1+(2*a1*N-f2)*kappa2-4*kappa1*kappa2-2*a3*N

Solve the first equation for kappa2:

>    kap2:=solve(eq1,kappa2);

kap2 := (a1*N-kappa1)*kappa1

Substitute this value of kappa2 into the second equation.

>    eq2a:=subs(kappa2=kap2,eq2);

eq2a := (f1*a1*N-f2*kappa1)*kappa1+(2*a1*N-f2)*(a1*N-kappa1)*kappa1-4*kappa1^2*(a1*N-kappa1)-2*a3*N

This equation for kappa1 is of third degree.  Look for asymptotic approximation of solution.

>    eq2b:=collect(expand(subs(kappa1=A*N+B+C/N,eq2a)),N);

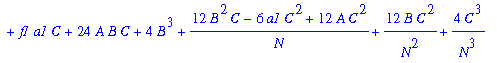
eq2b := (-6*a1*A^2+4*A^3+2*a1^2*A)*N^3+(12*A^2*B+f1*a1*A-f2*a1*A-12*a1*A*B+2*a1^2*B)*N^2+(12*A^2*C+f1*a1*B-2*a3+2*a1^2*C-f2*a1*B-6*a1*B^2-12*a1*A*C+12*A*B^2)*N-f2*a1*C-12*a1*B*C+f1*a1*C+24*A*B*C+4*B^3+...
eq2b := (-6*a1*A^2+4*A^3+2*a1^2*A)*N^3+(12*A^2*B+f1*a1*A-f2*a1*A-12*a1*A*B+2*a1^2*B)*N^2+(12*A^2*C+f1*a1*B-2*a3+2*a1^2*C-f2*a1*B-6*a1*B^2-12*a1*A*C+12*A*B^2)*N-f2*a1*C-12*a1*B*C+f1*a1*C+24*A*B*C+4*B^3+...
eq2b := (-6*a1*A^2+4*A^3+2*a1^2*A)*N^3+(12*A^2*B+f1*a1*A-f2*a1*A-12*a1*A*B+2*a1^2*B)*N^2+(12*A^2*C+f1*a1*B-2*a3+2*a1^2*C-f2*a1*B-6*a1*B^2-12*a1*A*C+12*A*B^2)*N-f2*a1*C-12*a1*B*C+f1*a1*C+24*A*B*C+4*B^3+...

Put the coefficients of N^3, N^2, N equal to zero!

>    eqA:=coeff(eq2b,N,3);

eqA := -6*a1*A^2+4*A^3+2*a1^2*A

>    eqB:=coeff(eq2b,N,2);

eqB := 12*A^2*B+f1*a1*A-f2*a1*A-12*a1*A*B+2*a1^2*B

>    eqC:=coeff(eq2b,N,1);

eqC := 12*A^2*C+f1*a1*B-2*a3+2*a1^2*C-f2*a1*B-6*a1*B^2-12*a1*A*C+12*A*B^2

>    AA:=solve(eqA,A);

AA := 0, a1, 1/2*a1

So there are three critical points. Renumber the three roots so that the A-value increases monotonically!

>    AA:=AA[1],AA[3],AA[2];

AA := 0, 1/2*a1, a1

The corresponding values of B and C are:

>    BB:=seq(solve(subs(A=AA[k],eqB),B),k=1..3);

BB := 0, 1/2*f1-1/2*f2, -1/2*f1+1/2*f2

>    CC:=seq(solve(subs(A=AA[k],B=BB[k],eqC),C),k=1..3);

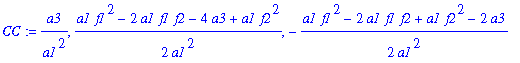
CC := a3/a1^2, 1/2*(a1*f1^2-2*a1*f1*f2-4*a3+a1*f2^2)/a1^2, -1/2*(a1*f1^2-2*a1*f1*f2+a1*f2^2-2*a3)/a1^2

The C-values at all three critical points depend on the unknown a3! So they are not used in the serquel.  

Determine the kappa2-values for each of the three critical points. The critical poins are denoted P1, P2, P3, in order of increasing A-values.

>    kap21:=seq(subs(kappa1=AA[k]*N+BB[k],kap2),k=1..3);

kap21 := 0, (1/2*a1*N-1/2*f1+1/2*f2)*(1/2*a1*N+1/2*f1-1/2*f2), (1/2*f1-1/2*f2)*(a1*N-1/2*f1+1/2*f2)

Note the different orders of magnitude for kappa2 at each of the three critical points...

Determine the jacobian matrix as a preparation to a study of the stabilities of the critical points.

>    P:=seq([AA[k]*N+BB[k],kap21[k]],k=1..3);

P := [0, 0], [1/2*a1*N+1/2*f1-1/2*f2, (1/2*a1*N-1/2*f1+1/2*f2)*(1/2*a1*N+1/2*f1-1/2*f2)], [a1*N-1/2*f1+1/2*f2, (1/2*f1-1/2*f2)*(a1*N-1/2*f1+1/2*f2)]
P := [0, 0], [1/2*a1*N+1/2*f1-1/2*f2, (1/2*a1*N-1/2*f1+1/2*f2)*(1/2*a1*N+1/2*f1-1/2*f2)], [a1*N-1/2*f1+1/2*f2, (1/2*f1-1/2*f2)*(a1*N-1/2*f1+1/2*f2)]

>    J:=Jacobian([eq1,eq2],[kappa1,kappa2]);

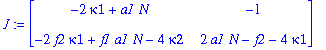
J := Matrix(%id = 6098076)

Determine the Jacobian at each critical point:

>    J1:=subs(kappa1=P[1][1],kappa2=P[1][2],J);

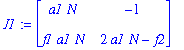
J1 := Matrix(%id = 6105564)

>    J2:=simplify(subs(kappa1=P[2][1],kappa2=P[2][2],J));

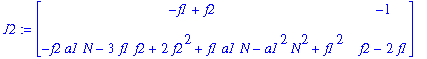
J2 := Matrix(%id = 6110072)

>    J3:=simplify(subs(kappa1=P[3][1],kappa2=P[3][2],J));

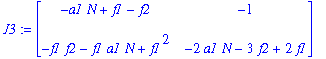
J3 := Matrix(%id = 6117108)

The eigenvalues of these three matrices are:

>    eg1:=Eigenvalues(J1);

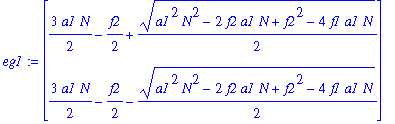
eg1 := Vector(%id = 5892684)

>    eg2:=Eigenvalues(J2);

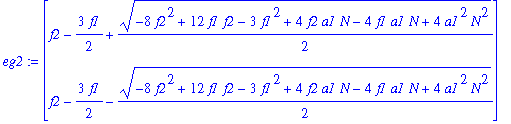
eg2 := Vector(%id = 6328756)

>    eg3:=Eigenvalues(J3);

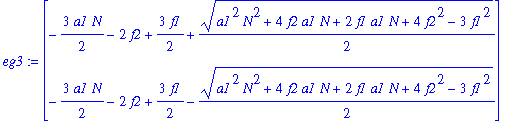
eg3 := Vector(%id = 5893364)

Determine asymptotic approximations of the eigenvalues:

>    assume(a1>0);

>    simplify(convert(asympt(eg1[1],N,1),polynom));

2*a1*N-f2-f1

>    simplify(convert(asympt(eg1[2],N,1),polynom));

a1*N+f1

The eigenvalues are asymptotic to K and 2K. Both are positive, so P1 is an unstable node.

>    simplify(convert(asympt(eg2[1],N,1),polynom));

a1*N+3/2*f2-2*f1

>    simplify(convert(asympt(eg2[2],N,1),polynom));

-a1*N+1/2*f2-f1

The eigenvalues are asymptotic to K and -K. One is positive and one is negative, so P2 is a saddle point.

>    simplify(convert(asympt(eg3[1],N,1),polynom));

-a1*N-f2+2*f1

>    simplify(convert(asympt(eg3[2],N,1),polynom));

-2*a1*N-3*f2+f1

The eigenvalues are asymptotic to -K and -2K. Both are negative, so P3 is a stable node.