![[Eigenvalues]](images/binomial31.gif){kind=small}
Determine the critical points of the first three moment closure equations for the Verhulst model, and their stabilities, under assumption of binomial distribution.
| > | restart; |
| > | with(LinearAlgebra,Eigenvalues); with(VectorCalculus,Jacobian); |
![[Jacobian]](images/binomial32.gif){kind=small}
The differential equations of the first three cumulants are equal to eq1, eq2, eq3prel.
| > | eq1:=(a1*N-kappa1)*kappa1-kappa2; |
| > | eq2:=(f1*a1*N-f2*kappa1)*kappa1+(2*a1*N-f2)*kappa2-4*kappa1*kappa2-2*kappa3; |
| > | eq3prel:=(a1*N-kappa1)*kappa1-6*f2*kappa1*kappa2-6*kappa1*kappa3+(3*f1*a1*N-1)*kappa2-6*kappa2^2+3*(a1*N-f2)*kappa3-3*kappa4; |
The assumption of binomial distribution means that kappa4=kappa2*(kappa1^2-6kappa1*kappa2+6kappa2^2)/kappa1^2.
| > | eq3:=collect(subs(kappa4=kappa2*(kappa1^2-6*kappa1*kappa2+6*kappa2^2)/kappa1^2,eq3prel),kappa1); |
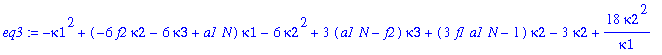
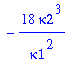
Solve the first equation for kappa2. This gives kappa2 as a function of kappa1.
| > | kap2:=solve(eq1,kappa2); |
Substitute this value of kappa2 into the second equation.
| > | eq2a:=subs(kappa2=kap2,eq2); |
Solve this equation for kappa3. This gives kappa3 as a function of kappa1.
| > | kap3:=solve(eq2a,kappa3); |
Insert the values of kappa2 and kappa3 into eq3 divided by minus 3. This gives an expression in kappa1.
| > | eq3a:=-map(simplify,collect(subs(kappa2=kap2,kappa3=kap3,eq3),kappa1))/3; |
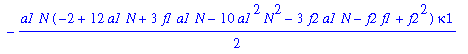
The problem now is to solve this third-degree equation in kappa1. (Some minor (cosmetic) simplification can be achieved by introducing K and sigma^2.) One root is equal to 0. It does not correspond to a critical point, since eq3 is not defined for kappa1=0.
The remaining 2 roots of eq3a satisfy the following second-degree equation:
| > | eq3b:=collect(eq3a/kappa1,kappa1); |
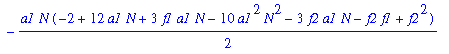
This equation can of course be solved explicitly. But I look instead for asymptotic approximations. Put kappa1 = AN + B + C/N.
| > | eq3c:=subs(kappa1=A*N+B+C/N,eq3b); |
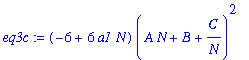
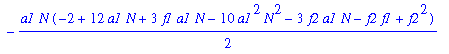
Form 3 equations (for A,B,C) by putting the coefficients of N^3, N^2, N^1 equal to zero.
| > | eqA:=coeff(eq3c,N,3); |
| > | eqB:=coeff(eq3c,N,2); |
| > | eqC:=coeff(eq3c,N,1); |
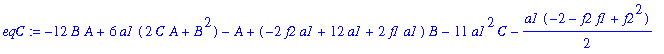
| > | AA:=solve(eqA,A); |
The A values of the 2 critical points are given by AA[1] and AA[2]. I expect AA[2] to correspond to a spurious solution.
Determine B and C-values corresponding to these 2 A-values: Begin with AA[1]:
| > | eqB1:=subs(A=AA[1],eqB); |
| > | BB[1]:=solve(eqB1,B); |
![BB[1] := 1/2*f2-1/2*f1](images/binomial323.gif){kind=small}
| > | eqC1:=simplify(subs(A=AA[1],B=BB[1],eqC)); |
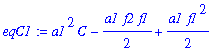
| > | CC[1]:=solve(eqC1,C); |
![CC[1] := 1/2*f1/a1*(f2-f1)](images/binomial325.gif){kind=small}
An asymptotic approximation for the first solution for kappa1 has thus been found. It is
AA[1]*N + BB[1] + CC[1]/N. Use it to derive asymptotic approximations of kappa2 and kappa3, using kap2 and kap3.
Write kappa2 sim DD[1]*N+EE[1] and kappa3 sim FF[1]*N.
| > | kap2; |
| > | kap21:=simplify(convert(asympt(subs(kappa1=AA[1]*N+BB[1]+CC[1]/N,kap2),N,2),polynom)); |
| > | DD[1]:=coeff(kap21,N,1); |
![DD[1] := -1/2*(f2-f1)*a1](images/binomial328.gif){kind=small}
| > | EE[1]:=factor(simplify(coeff(kap21,N,0))); |
![EE[1] := -1/4*(f2-f1)*(f2+f1)](images/binomial329.gif){kind=small}
| > | kap31:=simplify(map(simplify,convert(asympt(subs(kappa1=AA[1]*N+BB[1]+CC[1]/N,kap3),N,2),polynom))); |
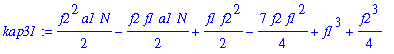
| > | FF[1]:=factor(coeff(kap31,N,1)); |
![FF[1] := 1/2*a1*f2*(f2-f1)](images/binomial331.gif){kind=small}
Now proceed to find approximations of the remaining critical point, with subscript 2. First I work on B and C.
| > | eqB2:=simplify(subs(A=AA[2],eqB)); |
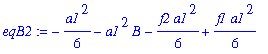
| > | BB[2]:=solve(eqB2,B); |
![BB[2] := -1/6-1/6*f2+1/6*f1](images/binomial333.gif){kind=small}
| > | eqC2:=simplify(subs(A=AA[2],B=BB[2],eqC)); |
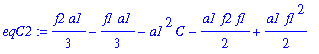
| > | CC[2]:=factor(solve(eqC2,C)); |
![CC[2] := -1/6*(-2+3*f1)*(f2-f1)/a1](images/binomial335.gif){kind=small}
| > | kap22:=simplify(convert(asympt(subs(kappa1=AA[2]*N+BB[2]+CC[2]/N,kap2),N,1),polynom)); |
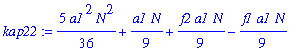
| > | DD[2]:=coeff(kap22,N,2); |
![DD[2] := 5/36*a1^2](images/binomial337.gif)
| > | EE[2]:=factor(coeff(kap22,N,1)); |
![EE[2] := 1/9*a1*(1+f2-f1)](images/binomial338.gif){kind=small}
So kappa2 is sim DD[2]*N^2 + EE[2]*N
| > | kap32:=simplify(convert(asympt(subs(kappa1=AA[2]*N+BB[2]+CC[2]/N,kap3),N,1),polynom)); |
| > | FF[2]:=coeff(kap32,N,3); |
![FF[2] := -5/54*a1^3](images/binomial340.gif)
And kappa3 = FF[2]*N^3.
I have now derived asymptotic approximations of the first three cumulants at each of the 2 critical points.
I would also like to study the local stability of the 2 critical points. I do this by evaluating the eigenvalues of the jacobian matrices evaluated at each of the four critical points...
| > | F:=[eq1,eq2,eq3]; |
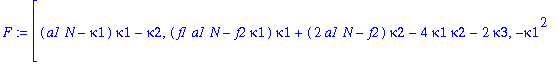
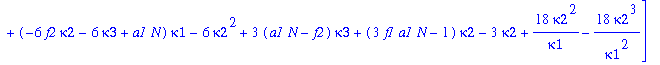
| > | J:=Jacobian(F,[kappa1,kappa2,kappa3]); |
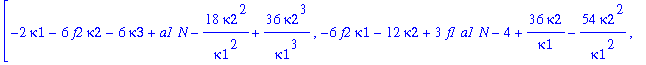
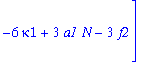
Determine the Jacobian in each of the two critical points:
| > | J1:=subs(kappa1=AA[1]*N+BB[1]+CC[1]/N,kappa2=DD[1]*N+EE[1],kappa3=FF[1]*N,J): |
| > | J2:=subs(kappa1=AA[2]*N+BB[2]+CC[2]/N,kappa2=DD[2]*N^2+EE[2]*N,kappa3=FF[2]*N^3,J): |
Determine the eigenvalues of the matrix J1. Maple on my PC takes too long time (for my patience) to find asymptotic approx of eigenvalues. So instead I modify the two matrices J1 and J2 by replacing each element by the first two elements of its asymptotic approximation as N approaches infinity. The modified matrices are named J1a and J2a.
| > | J1a:=J1: |
| > | J1a[1,1]:=convert(asympt(J1[1,1],N,1),polynom); |
![J1a[1,1] := -a1*N+f1-f2](images/binomial348.gif){kind=small}
| > | J1a[1,2]; |
| > | J1a[1,3]; |
| > | J1a[2,1]:=simplify(convert(asympt(J1[2,1],N,1),polynom)); |
![J1a[2,1] := -f1*a1*N+f2*f1-f1^2](images/binomial351.gif){kind=small}
| > | J1a[2,2]:=convert(asympt(J1[2,2],N,1),polynom); |
![J1a[2,2] := -2*a1*N-3*f2+2*f1](images/binomial352.gif){kind=small}
| > | J1a[2,3]; |
| > | J1a[3,1]:=simplify(convert(asympt(J1[3,1],N,4),polynom)); |
![J1a[3,1] := -a1*N-f2-9/2*f2^2+9*f2*f1-9/2*f1^2-3*f2^3-15*f2*f1^2+f1+27/2*f1*f2^2+9/2*f1^3](images/binomial354.gif)
| > | J1a[3,2]:=simplify(convert(asympt(J1[3,2],N,1),polynom)); |
![J1a[3,2] := -3*f1*a1*N-4-27/2*f2^2-33/2*f1^2+30*f2*f1-18*f2+18*f1](images/binomial355.gif)
| > | J1a[3,3]:=convert(asympt(J1[3,3],N,1),polynom); |
![J1a[3,3] := -3*a1*N-6*f2+3*f1](images/binomial356.gif){kind=small}
Determine the eigenvalues of the modified matrix J1a:
| > | a1:='a1': |
| > | eg1:=Eigenvalues(J1a): |
Determine asymptotic approximations of the eigenvalues of J1a:
| > | a1:='a1': |
| > | eg11a:=convert(asympt(eg1[1],N,3),polynom): |
| > | assume(a1>0); |
| > | eg11b:=simplify(evalc(eg11a)); |
| > | a1:='a1': |
| > | eg12a:=convert(asympt(eg1[2],N,3),polynom): |
| > | assume(a1>0); |
| > | eg12b:=simplify(eg12a); |
| > | a1:='a1': |
| > | eg13a:=convert(asympt(eg1[3],N,3),polynom): |
| > | assume(a1>0); |
| > | eg13b:=simplify(eg13a); |
| > | a1:='a1': |
The 3 eigenvalues are asymptotic to -K, -2K, -3K. All are negative. Hence this critical point is stable.
Proceed to modify the matrix J2:
| > | J2a:=J2: |
| > | J2a[1,1]:=convert(asympt(J2[1,1],N,1),polynom); |
![J2a[1,1] := -2/3*a1*N+1/3+1/3*f2-1/3*f1](images/binomial360.gif){kind=small}
| > | J2a[1,2]; |
| > | J2a[1,3]; |
| > | J2a[2,1]:=convert(asympt(J2[2,1],N,0),polynom); |
![J2a[2,1] := -5/9*a1^2*N^2+(-5/3*f2*a1+f1*a1-4/9*a1*(1+f2-f1))*N](images/binomial363.gif)
| > | J2a[2,2]:=convert(asympt(J2[2,2],N,1),polynom); |
![J2a[2,2] := -4/3*a1*N-1/3*f2+2/3-2/3*f1](images/binomial364.gif){kind=small}
| > | J2a[2,3]; |
| > | J2a[3,1]:=simplify(convert(asympt(J2[3,1],N,5),polynom)); |
![J2a[3,1] := 13/18*a1^3*N^3-1/3*a1^2*N^2*f2-1/2*a1^2*N^2*f1](images/binomial366.gif)
| > | J2a[3,2]:=simplify(convert(asympt(J2[3,2],N,0),polynom)); |
![J2a[3,2] := -19/6*a1^2*N^2+5/3*a1*N-28/3*f2*a1*N+22/3*f1*a1*N](images/binomial367.gif)
| > | J2a[3,3]:=convert(asympt(J2[3,3],N,1),polynom); |
![J2a[3,3] := -2*a1*N+1-2*f2-f1](images/binomial368.gif){kind=small}
The eigenvalues of the matrix J2a are:
| > | a1:='a1': |
| > | eg2:=Eigenvalues(J2a): |
Determine asymptotic approximations of the three eigenvalues of J2:
| > | a1:='a1': |
| > | eg21a:=convert(asympt(eg2[1],N,3),polynom): |
| > | assume(a1>0); |
| > | eg21b:=evalf(simplify(evalc(eg21a))); |
| > | a1:='a1': |
| > | eg22a:=convert(asympt(eg2[2],N,3),polynom): |
| > | assume(a1>0); |
| > | eg22b:=evalc(evalf(simplify(eg22a))); |
| > | a1:='a1': |
| > | eg23a:=convert(asympt(eg2[3],N,3),polynom): |
| > | assume(a1>0); |
| > | eg23b:=evalf(simplify(evalc(eg23a))); |
The eigenvalues are asymptotically 1.19K, -4.19K, -K. Hence the corresponding critical point is unstable.
| > |