sis2.mws

This Maple worksheet derives the diffusion approximation of a bivariate Markov population process that serves as an SIS model, accounting for differential death rate. NOTE that this model uses the conventional infection rate!

The file "abc.m" contains the three procedures equ, cov, denote used below. The source code for these procedures is contained in the Maple worksheet abc.mws

> restart;
with(linalg,matrix,jacobian);
read "C:/mydocu~1/ingemar/maple/desto/abc.m";
unprotect(gamma);

Reparametrize! Express old parameters in terms of new ones:

> gamma:=mu*(alpha1-delta1); mu1:=mu*(delta1-1); beta:=mu*alpha1*R0;

Transition rates of scaled state variables (x1=S/N, x2=I/N) are stored in a table:

> trans:=table([[1,0]=mu,[-1,1]=beta*x1*x2,[-1,0]=mu*x1,[0,-1]=(mu+mu1)*x2, [1,-1]=gamma*x2]);

The RHSs of the two deterministic equations are determined via the procedure equ:

> eq1:=equ(1,trans);
eq2:=simplify(equ(2,trans));

The local covariance matrix is determined via the procedure cov:

> Sx:=simplify(cov(trans));

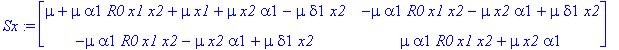
Critical points:

> crit:=[solve({eq1,eq2},{x1,x2})];

Denote the critical point that corresponds to an endemic level by x10, x20:

> xx:=denote(crit):
x10:=xx[1];
x20:=xx[2];

The Jacobian matrix:

> Bx:=simplify(jacobian([eq1,eq2],[x1,x2]));

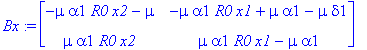
Evaluate the Jacobian at the critical point:

> B:=simplify(subs({x1=x10,x2=x20},evalm(Bx)));

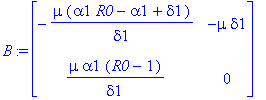
Evaluate the local covariance matrix at the critical point:

> S:=simplify(subs(x1=x10,x2=x20,evalm(Sx)));

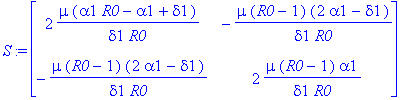
Now proceed to solve B*SIG+SIG*BT=-S:

> SIG:=matrix([[s11,s12],[s12,s22]]):

> A:=evalm(B&*SIG+SIG&*transpose(B)):

A and S are symmetric. Formulate three equations:

> e1:=A[1,1]=-S[1,1]: e2:=A[1,2]=-S[1,2]: e3:=A[2,2]=-S[2,2]:

Solve for the elements of the covariance matrix SIG:

> solve({e1,e2,e3},{s11,s12,s22});

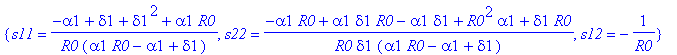
> assign(%);

Determine asymptotic approximations as becomes large. Use subscript a.

> s11a:=map(simplify,convert(asympt(s11,alpha1,2),polynom));
s12a:=s12;
s22a:=map(simplify,convert(asympt(s22,alpha1,2),polynom));

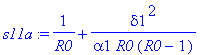
Compute mean and variance of x1+x2:

> m:=simplify(x10+x20);
v:=simplify(s11+s22+2*s12);
va:=map(simplify,convert(asympt(v,alpha1,2),polynom));
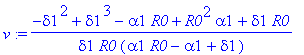