Tvåvariabelgränsvärden

När en tvåvariabelfunktion har en graf som liknar en spiraltrappa, kallar man den diskontinuitet som finns i trappans centralpunktl för spiraltrappsdiskontinuitet.Typiskt för spiraltrappsytor är ju att man befinner sig på olika nivåer på olika vägar in mot centralpunkten. På grund av detta får man slutsatsen att (tvåvariabel)gränsvärdet för funktionen inte existerar då punkterna närmar sig centralpunkten.

Funktionen arg(z) är kanske det klassiska exemplet.

Här är ett annat:

Grafen för z = f(x,y) = 3y²/(x²+y²):

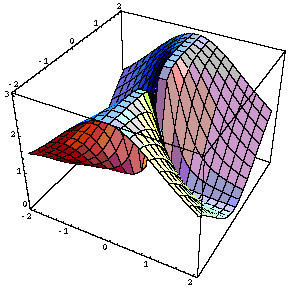
Om man inför polära koordinater i funktionsuttrycket ser man exakt vad gränsvärdena blir då man går in mot origo längs olika argumentvinklar :

x = r cos och y = r sin    ger x²+y² = r².

Man får alltså f(x,y) = 3sin² vilket visar att f(x,y) är konstant på räta linjer genom origo(och därmed får ett konstigt spiraltrappsliknande utseende nära origo) och att funktionsvärdena ligger i intervallet [0 , 3].
Förhoppningsvis går detta att urskilja i grafen ovan.

Däremot existerar ju inte tvåvariabelgränsvärdet då (x,y) -> (0,0) eftersom man för detta kräver att det skall vara oberoende av vägen.

I Ex 3 , s. 53 i kursboken finns ett liknande resonemang.

Detta problem med ickeexisterande tvåvariabelgränsvärden dyker upp i samband med att man försöker bilda z-derivator av komplexa funktioner av x och y.
Det visar sig att Cauchy-Riemanns ekvationer måste vara uppfyllda för att gränsvärdet och därmed derivatan skall existera.

Se också härledningen av Cauchy-Riemanns ekvationer i kursboken på s. 60-61. Där används villkoret att gränsvärdet skall vara oberoende av vägen på så sätt att man väljer ut två vägar, parallella med x-axeln och y-axeln. Och sedan drar man slutsatserna av att gränsvärdena längs dessa vägar (som ju svarar mot de partiella derivatorna med avseende på x resp. y) är lika.
Slutsatserna visar sig bli just C-R-ekvationerna.

Här finns ett alternativt sätt att lösa samma problem.