Detta är fortsättning från Gausselimination 1.
Där visades att om a inte är lika med 18
så finns en unik lösning.
Fallet a=18 svarar mot att systemets matris
har determinanten = 0 vilket betyder
att radvektorerna, planens normalvektorer,
är linjärt beroende dvs ligger i samma plan.
Därför framstår alla tre planen som linjer om man ser dem från ett visst håll.
I fall 1 (ingen lösning) ser det ut som till höger nedan.
I fall2 (skärningslinje, oändligt många lösningar) ser det ut som till vänster.)
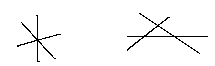 I fall 2 (som här svarar mot a=18 och b=-7/2) gäller det
alltså att räkna fram ekvationen för skärningslinjen.
I fall 2 (som här svarar mot a=18 och b=-7/2) gäller det
alltså att räkna fram ekvationen för skärningslinjen.
Genom att sätta z=t kan man få fram ekvationen på
parameterform.
|