Tavlan föreställde ett ovanligt långt och rakt järnvägsspår.

Den här bilden visar hur spåret hamnade på bildytan.

Konstnären, representerad av ett öga, befinner sig en längdenhet framför bildytan och avståndet mellan spårets syllar är är också en längdenhet.

Horisonten, sedd genom konstnärens öga, hamnar på höjden H i bilden medan syll nr n hamnar på höjden a_n.

Eftersom a_n/n = H/( n + 1) (likformiga trianglar) får man
a_n = H·n/(n + 1) .

Spårbilden kan därför användas som en illustration av talföljdsgränsvärdet (Vi sätter nu H=1) :

.

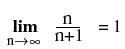Men man kan även se spåret som en summa av avstånden v_n mellan syllarna.

Eftersom v_n = a_n - a_n-1 = n/(n+1) - (n-1)/n = (n² - n² + 1)/n(n+1) = 1/n(n+1) blir summan av syllmellanrummen:

Tillbaka till järnvägstavlan.