Elias Jarlebring
Research description
Research field: numerical linear algebra
Along with experiment and theory, computation is nowadays widely recognized as a crucial component for modern research in science and engineering. Instead of carrying out experiments, which can be expensive and time-consuming, a prediction using an advanced simulation on a computer can be much cheaper and time-efficient. At some point in such a research process we often face a formulation or characterization using the mathematical concepts of matrices, vectors and theory from linear algebra. My research interest consists of all aspects related to scientific computing and numerical analysis, and my main research contributions have been on the study of numerical analysis for linear algebra operations, also known as numerical linear algebra or matrix computations.
Due
to the fact
that numerical linear algebra
appears in a wide variety of fields,
it has an unusual role as
a very interdisciplinary subject
and
my research has involved topics
in a number of related fields, such as
systems and control, quantum mechanics, optimization and
some applications in mechanical engineering.
Selection of current projects
Iterative methods for nonlinear eigenvalue problems
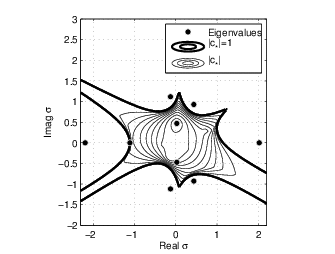
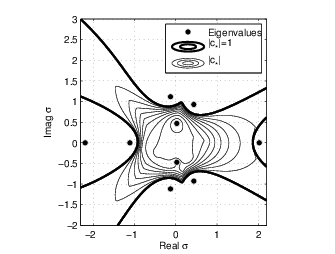
In many situations, a discretization of a partial differential equation and a linearization lead to the problem of computing eigenvalues of a large matrix. In contrast to this, in this project derive and study algorithms for new types of eigenvalue problems which are nonlinear, thereby providing the possibility to study new recent types of physical models. The project involves algorithms, theory, applications and software. The new algorithms are analyzed and developed with tools from numerical linear algebra and complex analysis, in particular Krylov methods and the theory for analytic functions. The algorithms are used to study specific problems in acoustics, in particular models of waveguides, and also problems in quantum mechanics and quantum chemistry.Example of description of convergence as a function of a parameter for two choices of the Rayleigh-quotient vectors (E. Jarlebring and W. Michiels, Analyzing the convergence factor of residual inverse iteration, BIT numerical mathematics, 51(4):937-957, 2011). The iterative method is convergent for all values inside the thick contour:
Example of a solution to the Gross-Pitaevskii equation computed with the iterative method in E. Jarlebring, S. Kvaal and W. Michiels, An inverse iteration method for eigenvalue problems with eigenvector nonlinearities, SIAM J. Sci. Comput., 2014:
Related publications:
- R. Van Beeumen, E. Jarlebring and W. Michiels
A rank-exploiting infinite Arnoldi algorithm for nonlinear eigenvalue problems
Numer. Linear Algebra Appl., 23(4):607-628, 2016 - E. Jarlebring, S. Kvaal and W. Michiels
An inverse iteration method for eigenvalue problems with eigenvector nonlinearities
SIAM J. Sci. Comput., 36-4:A1978-A2001, 2014 - E. Jarlebring, K. Meerbergen and W. Michiels
Computing a partial Schur factorization of nonlinear eigenvalue problems using the infinite Arnoldi method
SIAM J. Matrix Anal. Appl., 35(2):411-436, 2014 - E. Jarlebring, W. Michiels and K. Meerbergen
A linear eigenvalue algorithm for the nonlinear eigenvalue problem
Numerische Mathematik, 122(1):169-195, 2012 - E. Jarlebring and W. Michiels
Analyzing the convergence factor of residual inverse iteration
BIT numerical mathematics, 51(4):937-957, 2011 - E. Jarlebring, K. Meerbergen and W. Michiels
A Krylov method for the delay eigenvalue problem
SIAM J. Sci. Comput., 32(6):3278-3300, 2010 - E. Jarlebring
Convergence factors of Newton methods for nonlinear eigenvalue problems
Linear Algebra Appl., 436:3943-3953, 2012 - E. Jarlebring and H. Voss
Rational Krylov for Nonlinear Eigenproblems, an Iterative Projection Method
Applications of Mathematics, 50(6):543-554, 2005
Computational solutions for time-delay systems
When external forces act on a real-world system, say a mechanical object, a chemical process, a control device in a factory or the gravitation from the sun acting on earth, the reaction often does not take place instantaneously. This situation appears for many phenomena in, e.g., engineering, biology and chemistry. In these situations, the system and the non-instantaneous action can be naturally modeled using a differential equation with a time delay also known as a delay-differential equation. In a simplified case, this is mathematically described by \[ \dot{x}(t)=A_0x(t)+A_1x(t-\tau_1). \] In the field of systems and control, one usually also consider an input function u and an output function y, \begin{align}\dot{x}(t)&=A_0x(t)+A_1x(t-\tau_1)+Bu(t)\\ y(t)&=Cx(t). \end{align} I have contributed to the following problems and fields:- Compute eigenvalues which are solutions to a nonlinear eigenvalue problem
- Computing and characterize stability by computing conditions such that there is an imaginary eigenvalue
- Compute the ℋ₂ norm of a time-delay systems
- Stability of a machine-tool milling model
- Model reduction techniques for time-delay systems based on balanced truncation, dominant pole selection and moment matching
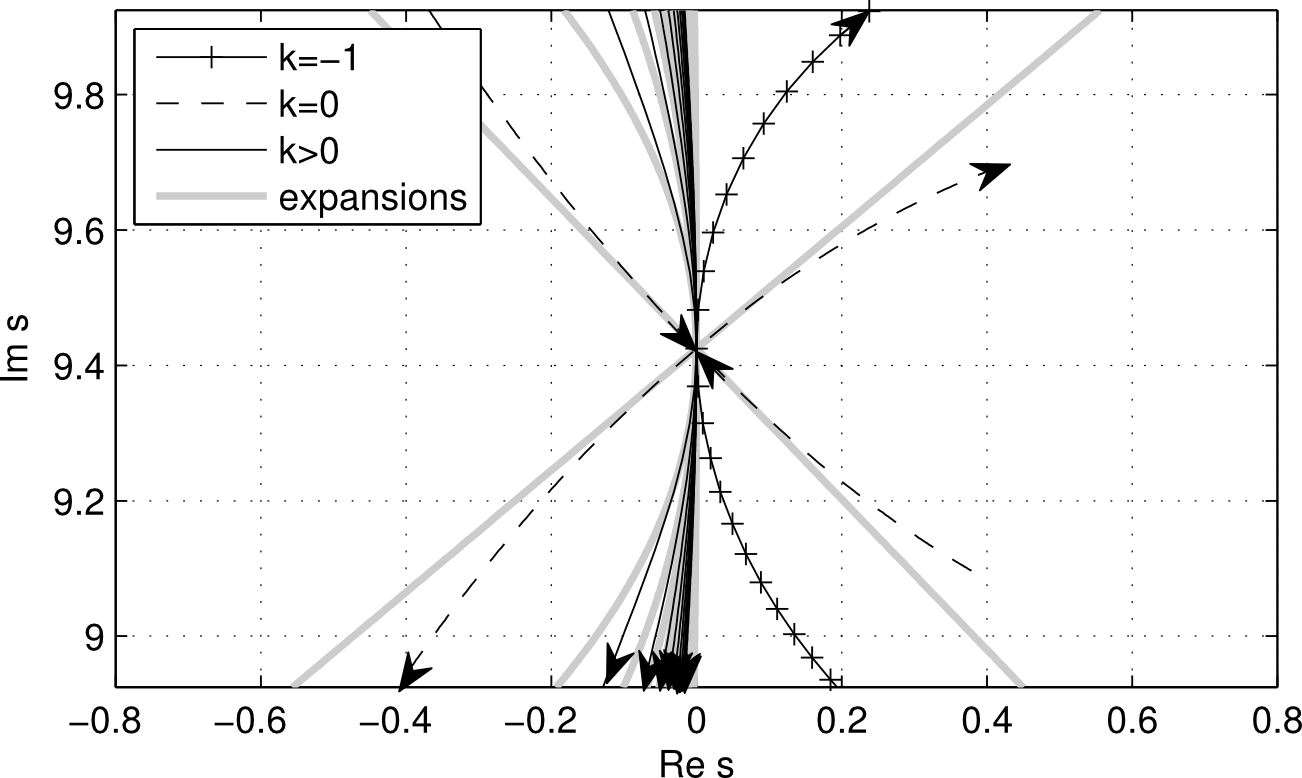
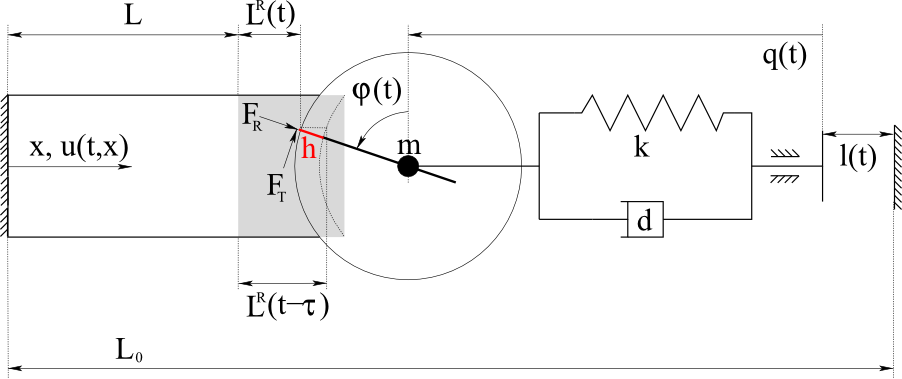
Example of description of stability with manually computed eigenvalues and the expansion from theory with an application from machine tool milling:
Related publications:
- E. Jarlebring, T. Damm and W. Michiels
Model reduction of time-delay systems using position balancing and delay Lyapunov equations
Mathematics of Control, Signals, and Systems, 25(2):147-166, 2013 - M. Saadvandi, K. Meerbergen and E. Jarlebring
On dominant poles and model reduction of second order time-delay systems
Appl. Numer. Math., 62(1):21-34, 2012 - J. Vanbiervliet, W. Michiels and E. Jarlebring
Using spectral discretization for the optimal ℋ₂ design of time-delay systems
Int. J. Control, 84(2):228-241, 2011 - E. Jarlebring, J. Vanbiervliet and W. Michiels
Characterizing and computing the ℋ₂ norm of time-delay systems by solving the delay Lyapunov equation
IEEE Trans. Autom. Control, full paper, 56(4):814-825, 2011 - W. Michiels, E. Jarlebring and K. Meerbergen
Krylov-based model order reduction of time-delay systems
SIAM J. Matrix Anal. Appl., 32(4):1399-1421, 2011 - E. Jarlebring, W. Michiels, K. Meerbergen
The infinite Arnoldi method and an application to time-delay systems with distributed delays
chapter in edited volume, in In R. Sipahi, T. Vyhlidal, P. Pepe, S.-I. Niculescu, Eds., 'Time Delay Systems - Methods, Applications and New Trends' - E. Jarlebring, K. Meerbergen and W. Michiels
A Krylov method for the delay eigenvalue problem
SIAM J. Sci. Comput., 32(6):3278-3300, 2010 - E. Jarlebring and W. Michiels
Invariance properties in the root sensitivity of time-delay systems with double imaginary roots
Automatica, 46:1112-1115, 2010 - E. Jarlebring
Critical delays and Polynomial Eigenvalue Problems
J. Comput. Appl. Math., 224(1):296-306, 2009 - E. Jarlebring and T. Damm
The Lambert W function and the spectrum of some multidimensional time-delay systems
Automatica, 43(12):2124-2128, 2007 - E. Jarlebring
The spectrum of delay-differential equations: numerical methods, stability and perturbation.
PhD thesis, Inst. Comp. Math, TU Braunschweig, 2008
Computational methods and applications for multiparameter and double eigenvalue problems
This project concerns the problem of determining choices of the scalar parameter μ such that the matrix A+μB has a double eigenvalue. The problem occurs in several fields in science, and particular attention is given to problems in quantum chemistry. In particular, we construct a method to accurately find all such solutions accurately. The method is based on characterizing the solution as an approximation of a two-parameter eigenvalue problem which can be solved accurately with methods available in the literature. Other properties of double eigenvalues and two-parameter eigenvalue problems are also studied.Related publications:
- E. Jarlebring, S. Kvaal and W. Michiels
Computing all pairs (λ,μ) such that λ is a double eigenvalue of A+μB
SIAM J. Matrix Anal. Appl., 32(3):902-927, 2011 - S. Kvaal, E. Jarlebring and W. Michiels
Computing singularities of perturbation series
Phys. Rev. A, 83:032505, 2011 - E. Jarlebring and W. Michiels
Invariance properties in the root sensitivity of time-delay systems with double imaginary roots
Automatica, 46:1112-1115, 2010 - E. Jarlebring and M.E. Hochstenbach
Polynomial two-parameter eigenvalue problems and matrix pencil methods for stability of delay-differential equations
Linear Algebra Appl., 431(3-4):369-380, 2009