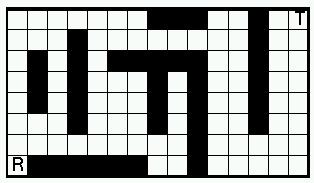
Roboten ska nu försöka hitta en väg från
R till T. Låt oss använda följande enkla strategi:
- Om möjligt, gå i godtycklig riktning mot målet. Med kartan ovan innebär det åt höger eller uppåt.
- Om det inte går att gå mot målet, gå i en annan godtycklig riktning.

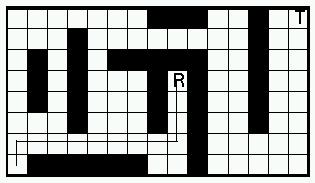
Roboten har nu kommit till en återvändsgränd
och måste vända om. Den följer då sitt eget spår
bakåt tills den kommer till en ruta där ett annat vägval är
möjligt. Notera att förutom de rutor roboten "backar" genom i detta
läge ska den aldrig gå in i rutor där den tidigare varit.
Gjorde den det skulle den kunna hamna i en evig loop. För att veta att
den inte återbesöker rutor måste roboten markera de rutor
den varit i. Dessa får vara gråa i kartan. Bilden nedan visar
kartan när roboten backat tillbaks ur återvändsgränden
och valt en ny väg. Egentligen skulle även de rutor som strecket
som visar robotens färdväg går genom varit gråa. För
att bilden ska bli tydligare får det räcka med att strecket visar
att roboten varit där.
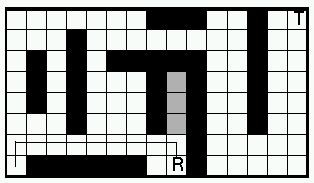

Vi kan nu lägga till ytterligare två regler till
strategin roboten använder för att hitta en väg.
- Markera alla rutor roboten går in i. Det är aldrig tillåtet att återvända till en sådan ruta utom enligt regel 4.
- När roboten hamnar i en återvändsgränd ska den gå tillbaks samma väg den kom tills den har möjlighet att gå till en ruta den inte tidigare varit i.

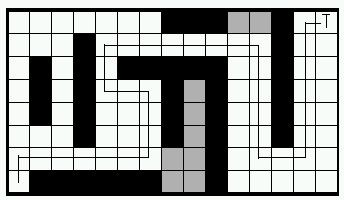
Nu vet roboten hur den ska nå målet och kan
börja flytta sig dit.
Definition av backtracking: Gå så långt som möjligt mot lösningen och kom ihåg de beslut som fattas längs vägen. I exemplet görs det genom att rita strecket som visar robotens väg. När det inte går att komma längre, backa tillbaks tills det går att fatta ett annat beslut. Detta illustreras av den tredje bilden uppifrån.
Det faktum att vi gråmarkerade rutor där roboten tidigare befunnit sig hade alltså inget med backtracking att göra (vilket inte hindrar att det var en bra idé).
När ett problem ska lösas med hjälp av backtracking krävs det nästan alltid någon form av datastruktur för att spara information om de beslut som fattas. I robotexemplet ovan blir det en datastruktur som representerar robotens väg genom rummet, tex en sekvens av struct ar som innehåller koordinater.
Backtracking kan användas både i iterativa och i rekursiva algoritmer. I en iterativ algoritm kommer det att krävas ytterligare en datastruktur för att spara sekvensen av beslut, ofta passar en stack bra. Roboten kan tex pusha en ny koordinat på stacken varje gång den går till en ny ruta och popa en koordinat när den måste backa. I en rekursiv algoritm behövs ingen sådan stack, det är själva följden av metodanrop som anger ordningen. I fallet med roboten kan den rekursiva metoden ha en lokal variabel som representerar aktuell position.
Definition av backtracking: Gå så långt som möjligt mot lösningen och kom ihåg de beslut som fattas längs vägen. I exemplet görs det genom att rita strecket som visar robotens väg. När det inte går att komma längre, backa tillbaks tills det går att fatta ett annat beslut. Detta illustreras av den tredje bilden uppifrån.
Det faktum att vi gråmarkerade rutor där roboten tidigare befunnit sig hade alltså inget med backtracking att göra (vilket inte hindrar att det var en bra idé).
När ett problem ska lösas med hjälp av backtracking krävs det nästan alltid någon form av datastruktur för att spara information om de beslut som fattas. I robotexemplet ovan blir det en datastruktur som representerar robotens väg genom rummet, tex en sekvens av struct ar som innehåller koordinater.
Backtracking kan användas både i iterativa och i rekursiva algoritmer. I en iterativ algoritm kommer det att krävas ytterligare en datastruktur för att spara sekvensen av beslut, ofta passar en stack bra. Roboten kan tex pusha en ny koordinat på stacken varje gång den går till en ny ruta och popa en koordinat när den måste backa. I en rekursiv algoritm behövs ingen sådan stack, det är själva följden av metodanrop som anger ordningen. I fallet med roboten kan den rekursiva metoden ha en lokal variabel som representerar aktuell position.