Analys av algoritmer
Eftersträvansvärda egenskaper hos en algoritm är:
- Lättförstådd (välkänd)
- Kod som är lätt att skriva och underhålla
- Hög exekveringshastighet
- Liten minnesåtgång
Alla är viktiga, men det här kapitlet handlar bara om exekveringshastighet.
Komplexitetsfunktioner
Definition: Komplexitetsfunktion T(n) anger hur många operationer
algoritmen utför för n indata. Som exempel betraktar vi följande
funktion
int rutin(int n){
int svar=0;
for(i=1;i<3*n;i++)
svar += i;
return svar;
}
Denna funktion har komplexitetsfunktionen T(n) = 3n·c1
+ c2. 3n kommer av att loopen körs 3·n varv. Konstanterna
c1 och c2 är den tid instruktionerna (addition, deklaration osv) tar.
Dessa konstanter kan vi inte beräkna eftersom de är beroende av
vilken kompilator vi har och vad vi har för dator. Vi är inte heller
intresserade av att ta fram T(n) så noga att vi kan tala om exakt hur
lång tid algoritmen tar att exekvera. Det vi är intresserade av
är storleksordningen av T(n), O(T(n)). Vad gäller detta exempel
är O(T(n)) = O(n). Det innebär att den dominerande termen (dvs den
som växer snabbast då n växer) i T(n) är proportionell
mot n. Att denna lilla funktion har en komplexitetsfunktion som är proportionell
mot n gäller alltid, oavsett kompilator osv. Det innebär att vi
alltid kan betrakta den som snabbare än funktioner som har tex O(n
2) och långsammare än funktioner som har O(1), dvs konstant
exekveringshastighet. Däremot vet vi inget om hur den är jämfört
med andra funktioner som också har O(n).
Vi kan tala om tre olika sorter av komplexitetsfunktion:
- W(n), worst case Den längsta tid det kan ta att exekvera
algoritmen. Den är intressant eftersom den ger oss en övre gräns
som aldrig överskrids. Den är dessutom ofta lätt att beräkna.
Problemet är att den kan ge en missvisande bild av algoritmen om den
sällan inträffar.
- A(n), genomsnittet Ger den sannaste bilden av algoritmens exekveringshastighet.
Vi måste dock vara medvetna om att det ibland kan gå mycket långsammare.
Den är ofta svårare att beräkna än W(n).
- B(n), best case Den är ointressant.
Låt oss som exempel räkna ut de tre komplexitetsfunktionerna
för nedanstående kod, vilken hittar ett tal i en lista av n element:
for(i=0;i<n;i++){
if(k==v[i])
return i;
}
return n;
- Worst case inträffar när det tal vi söker ligger
sist i listan. Det hittar vi när i har antagit alla värden
från 0 till n-1. W(n) = c1·n + c2
. O(W(n)) = O(n).
- Best case inträffar när det sökta talet ligger
först i listan. B(n) = c3. O(B(n)) = O(1).
- Genomsnittet är medelvärdet av exekveringstiden för
att söka efter ett tal på alla olika platser i listan. A(n) =
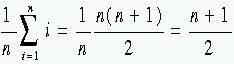 och O(A(n)) = O(n). För att räkna ut A(n) var vi tvugna att beräkna
summan. Detta är egentligen onödigt eftersom vi bara är intresserade
av O(A(n)) vilken ofta kan listas ut utan beräkningar. I det här
fallet kan vi tänka oss att den genomsnittliga exekveringstiden
sker när det sökta elementet ligger någonstans i mitten av
listan. Då är A(n) = c4·n/2 + c5 och
O(A(n)) = O(n).
och O(A(n)) = O(n). För att räkna ut A(n) var vi tvugna att beräkna
summan. Detta är egentligen onödigt eftersom vi bara är intresserade
av O(A(n)) vilken ofta kan listas ut utan beräkningar. I det här
fallet kan vi tänka oss att den genomsnittliga exekveringstiden
sker när det sökta elementet ligger någonstans i mitten av
listan. Då är A(n) = c4·n/2 + c5 och
O(A(n)) = O(n).
Hur snabbt växer olika funktioner?
Eftersom vi är intresserade av den dominerande termen i komplexitetsfunktionen
måste vi veta hur snabbt olika funktioner växer med n. I ordning
från snabbast till långsammast växande gäller följande
(se tabell på sid 126): n! > cn > nc >
n·log(n) > n > log(n) > 1.
Exempel
Bubbelsort
Vi ska nu analysera en sorteringsalgoritm som kallas bubbelsort. Om en lista
ska sorteras i stigande ordning börjar vi med att jämföra det
första elementet med alla andra element och placera in det så att
alla mindre element ligger före. Sedan gör vi samma sak med det
andra elementet osv. I C kan det se ut så här:
for(i=0; i<n-1; i++)
for(j=i+1; j<n; j++)
if(v[i] > v[j] ) {
temp = v[j];
v[j] = v[i];
v[i]=temp;
}
}
}
Vi har två nästlade loopar. För båda gäller
att antalet varv de exekveras är proportionellt mot n. För vart
och ett av de n varven i den yttre loopen går alltså den inre
loopen i storleksordningen n varv. Detta ger att O(B(n)) = O(A(n)) = O(W(n))
= O(n2). Det innebär inte att B(n) = A(n) = W(n) eftersom
tilldelningarna i if-satsen görs olika många gånger i de
tre fallen.
Vill vi vara mer formella gäller följande (vilket ger samma resultat):
O(B(n)) = O(A(n)) = O(W(n)) = 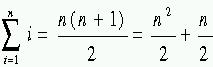 = O(n2).
= O(n2).
Tornen i Hanoi
Till sist analyserar vi en rekursiv algoritm, tornen i Hanoi, se bilden
på sid 133. Uppgiften är att flytta alla brickor till en annan
pinne. En större bricka får aldrig placeras ovanpå en mindre.
Lösningen är som följer (n brickor ska flyttas från
pinne f till pinne t. x är den tredje pinnen):
int hanoi(int n, int f, int t, int x) {
if (n > 0) {
hanoi(n-1, f, x, t);
hanoi(n-1, x, t, f);
}
}
Här gäller (eftersom funktionen innehåller två rekursiva
anrop med n-1) att O(T(n)) = O(2·T(n-1)) = O(2·2·T(n-2))
= O(2·2·2·T(n-3)) = ... = O(2n·T(n-n))
= O(2n·T(0)) = O(2n·c) = O(2n
).
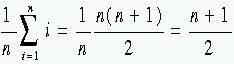 och O(A(n)) = O(n). För att räkna ut A(n) var vi tvugna att beräkna
summan. Detta är egentligen onödigt eftersom vi bara är intresserade
av O(A(n)) vilken ofta kan listas ut utan beräkningar. I det här
fallet kan vi tänka oss att den genomsnittliga exekveringstiden
sker när det sökta elementet ligger någonstans i mitten av
listan. Då är A(n) = c4·n/2 + c5 och
O(A(n)) = O(n).
och O(A(n)) = O(n). För att räkna ut A(n) var vi tvugna att beräkna
summan. Detta är egentligen onödigt eftersom vi bara är intresserade
av O(A(n)) vilken ofta kan listas ut utan beräkningar. I det här
fallet kan vi tänka oss att den genomsnittliga exekveringstiden
sker när det sökta elementet ligger någonstans i mitten av
listan. Då är A(n) = c4·n/2 + c5 och
O(A(n)) = O(n).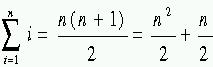 = O(n2).
= O(n2).