Slumptal
Användningsområden
- Indata vid testning av program (prestanda och funktion)
- Simuleringar av verkliga förlopp, tex kunder som kommer in i
en bank. Hur länge får de vänta? Hinner kassören
med?
- Slumpfaktor i algoritmer, tex öppningsdrag i spel eller väntetid
vid kollision på nätet.
Är det verkligen slump?
Kan en dator verkligen göra beräkningar med slumpmässigt
resultat? Nej, lyckligtvis inte. De slumptal vi kan generera är alltså
inte äkta slumptal. Slumptalssekvenser genereras enligt något
i den här stilen: Välj ett första "slumptal" , x0
. Övriga slumptal beräknas enligt någon bestämd
formel, tex x i = (e + xi-1)5. Vet vi
ett slumptal kan vi räkna ut nästa om vi känner algoritmen
enligt vilken slumptalen genereras. Detta kallas pseudoslumptal. Motsatsen
är äkta slump, tex atomers sönderfall (eller en lottodragning?).
Eftertraktade egenskaper
Om vi nu inte kan generera äkta slumptal vill vi i alla fall
att våra pseudoslumptal ska ha egenskaper som liknar äkta slumptal,
de ska vara så oförutsägbara som möjligt. Vi eftersträvar
därför detta:
- Alla slumptal ska vara lika sannolika, dvs de ska vara rektangulärfördelade.
Genererar vi en stor mängd slumptal mellan tex 1 och 10 förväntar
vi oss att det ska finnas ungefär lika många av alla. OBS! Att
alla är lika sannolika betyder inte att alla alltid förekommer
exakt lika många gånger. Gjorde de det skulle de vara extremt
förutsägbara.
- Samma sekvens av slumptal får inte genereras varje gång
programmet körs. Eftersom alla slumptal kommer att räknas
ut med hjälp av det föregående slumptalet måste vi
ha olika startvärden, kallas frö, varje gång serien
genereras. Vanligtvis används datorns klocka som frö.
- Sekvensen ska ha en lång period. Varje slumptal är
(utan någon som helst slump) uträknat utifrån föregående
slumptal. Detta innebär att när vi får fram ett slumptal
som förekommit tidigare i sekvensen har vi hamnat i en loop, sekvensen
kommer att upprepa sig . Sekvensens period är ett mått på
loopens längd.
- Ett slumptal ska inte alltid följas av samma slumptal.
Betrakta sekvensen 0 4 17 20 5 0 13 8. Talet noll följs inte alltid
av samma tal. Detta är förstås bra eftersom talen blir mer
oförutsägbara.
Slumptal i C
Följande funktioner (definierade i stdlib.h) är vanliga
i C:
- int rand() Returnerar ett slumpmässigt heltal i intervallet
[0, RAND_MAX]. RAND_MAX är också definierad
i stdlib.h och är förmodligen lika med den största int
:en.
- int random(int num) Returnerar ett slumptal i intervallet
[0, num-1].
- srand(unsigned int seed) Anger fröet, dvs första
värdet, för de slumptal som sedan returneras av rand()
.
- randomize() Ett (bättre?) alternativ till srand()
. Anger datorns klocka som frö.
Observera att det är olämpligt att sätta ett frö
flera gånger per exekvering, speciellt om fröet är baserat
på tiden. Detta riskerar ge upphov till att samma sekvens repeteras.
Slumptalsgeneratorer
Det är omöjligt att bevisa att en viss algoritm ger en bra
sekvens av slumptal. Genom beräkningar och tester har man kommit fram
till två olika typer av algoritmer som fungerar bra.
Linjärt genererade slumptal
Dessa genereras enligt formeln xn = (axn-1 +
c) mod m. Perioden kan uppenbarligen inte bli större än m, men
tyvärr blir den inte alltid ens så stor. Värden på
konstanterna a, c och m som visat sig fungera bra finns på sid 105
i kompendiet. Här kommer ett exempel med Park-Millers konstanter,
Linear.c
. Det är i princip samma exempel som finns på sid 106.
Skillnaden är framför allt att genom att använda unsigned
long i stället för long förhindrar vi
att kompilatorn tolkar skiftoperationerna som division/multiplikation
med två i stället för som bitmanipulering. Skillnaden
är denna:
Antag att vi ska högerskifta värdet -1 ett steg. Vi har
alltså: -1 = 11111111 111111112. Ett stegs högerskift
ger: -1 >> 1 = 01111111 111111112 = 3276810
. Om kompilatorn skulle få för sig att det är en division
vi vill utföra kommer den att ge resultatet av -1/2 = 010
= 00000000 00000000 2 .
Notera att med så pass stora värden på a och m som
i detta exempel är vi tvugna att dela upp fröet i två
delar eftersom a * (m-1) inte ryms i en long. Hade a och m varit
mindre hade vi sluppit bitmanipuleringen.
Det är en slumptalsgenerator av denna typ som finns i Borland
C. Dess fördel är, förutom att ge en bra slumptalssekvens,
framför allt att den kräver lite minne. Den är dessutom
hyfsat snabb.
Additativt genererade slumptal
Dessa genereras på följande sätt, xn =
(x n-j + xn-k) mod m. Bra värden på
konstanterna är j = 24, k = 55 och m = 2^31. Denna algoritm är
snabbare än föregående eftersom den innehåller färre
operationer (en multiplikation mindre). Däremot kräver den mer
minnesutrymme eftersom vi måste hålla 55 gamla värden
i minnet. Vi får också problemet att generera 55 startvärden.
Problemet att ett slumptal alltid följs av samma slumptal
Oavsett om slumptalen genereras additativt eller linjärt vet
vi att vi är inne i en loop när ett visst tal dyker upp andra
gången. Därefter är sekvensen helt identisk med förra
varvet i loopen, dvs extremt förutsägbar. Detta kan vi lösa
på följande sätt. Om vår slumptalsgenerator genererar
slumptalssekvensen x n låter vi den inte returnera x
n utan i stället yn = xn / d, där
d är en konstant. Antag att följande sekvens av xn
genereras, 50, 7, ..., 51, 93, ..., 50, 7. När värdet 50 dyker
upp andra gången är vi inne i en loop och exakt samma sekvens
följer igen. Men betrakta nu y n om d=2: 25, 3, ..., 25,
46, ..., 25, 3!!! Visserligen blev perioden inte längre och vi får
bara hälften så många olika tal, men det går inte
längre att förutsäga något om sekvensens fortsättning
bara för att samma tal dyker upp andra gången. I exemplet följs
25 första gången av 7 och andra gången av 46.
Test av slumptalsgeneratorer
Nu ska vi titta på tre olika sätt att undersöka
kvalitén hos en slumptalssekvens.
Chi-2
Detta test undersöker om alla slumptal är lika sannolika.
Antag att vi simulerar tärningskast. Är det troligt att resultaten
av 1200 kast fördelar sig så här? 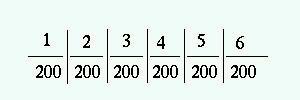 Nej, knappast. Kan det vara så att om vi kastar tillräckligt
många gånger är det säkert att resultaten blir så
jämnt fördelade? Nej, inte det heller för då skulle
resultatet av det sista kastet vara förutbestämt ("slumpen har
inget minne"). Ett troligare resultat av 1200 kast med tärningen
är nog detta:
Nej, knappast. Kan det vara så att om vi kastar tillräckligt
många gånger är det säkert att resultaten blir så
jämnt fördelade? Nej, inte det heller för då skulle
resultatet av det sista kastet vara förutbestämt ("slumpen har
inget minne"). Ett troligare resultat av 1200 kast med tärningen
är nog detta: 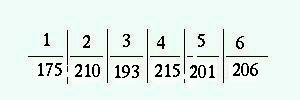 Innebär det att alla resultat är lika sannolika? Det är
den frågan som besvaras av Chi2-testet. Varje kast med tärningen
resulterar i ett utfall (1-6). Betrakta varje utfall som en hink. När
alla kast har gjorts vet vi hur många utfall som hamnade i varje
hink. Sedan beräknar vi summan Q av kvadraten på skillnaden
mellan förväntat och verkligt utfall dividerat med förväntat
utfall,
Innebär det att alla resultat är lika sannolika? Det är
den frågan som besvaras av Chi2-testet. Varje kast med tärningen
resulterar i ett utfall (1-6). Betrakta varje utfall som en hink. När
alla kast har gjorts vet vi hur många utfall som hamnade i varje
hink. Sedan beräknar vi summan Q av kvadraten på skillnaden
mellan förväntat och verkligt utfall dividerat med förväntat
utfall, 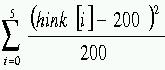 , se sid 108. I vårt exempel blir Q = 5,18. Nu är det dags
för en titt i tabellen på sid 109. Raderna representerar antalet
frihetsgrader , dvs antalet hinkar -1, 5 i vårt exempel.
Kolumnerna anger hur många procents sannolikhet det är att Q
ska vara mindre än ett visst värde. Med fem frihetsgrader är
det sannolikheten 75% att Q är mindre än 6,626 och 50% sannolikhet
att Q är större än 4,351. Det finns ingen anledning att misstänka
att tärningen/slumptalsgeneratorn är felaktig. Det är vad
ett Chi2-test kan säga oss.
, se sid 108. I vårt exempel blir Q = 5,18. Nu är det dags
för en titt i tabellen på sid 109. Raderna representerar antalet
frihetsgrader , dvs antalet hinkar -1, 5 i vårt exempel.
Kolumnerna anger hur många procents sannolikhet det är att Q
ska vara mindre än ett visst värde. Med fem frihetsgrader är
det sannolikheten 75% att Q är mindre än 6,626 och 50% sannolikhet
att Q är större än 4,351. Det finns ingen anledning att misstänka
att tärningen/slumptalsgeneratorn är felaktig. Det är vad
ett Chi2-test kan säga oss.
Naturligtvis blir Chi2-testet mer tillförlitligt desto fler gånger
tärningen kastas. För att det ska vara ett meningsfullt test
ska varje utfall ha ett förväntat värde >= 5. Tärningen
måste alltså kastas minst 30 gånger.
Gap test
I detta test kollar vi att det i genomsnitt är ett rimligt avstånd
(gap) i sekvensen mellan två slumptal som är inom ett visst
intervall. Det vi vill försäkra oss om är att slippa en serie
med ett tydligt mönster, tex 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4,
4, .... Detta testas med hjälp av ett Chi2-test där hinkarna är
det förväntade avståndet mellan de två talen.
Antag att vi ska test en slumptalsgenerator som genererar tal i intervallet
[0, 1[. Vi undersöker avståndet mellan tal som är tex i
intervallet [0.1, 0.3[. Sannolikheten att ett tal ska vara inom intervallet
är p = 0, 3 - 0, 1 = 0,2 och sannolikheten att det inte ska vara inom
intervallet är 1 - p = 1 - 0,2 = 0,8. Sannolikheten att avståndet
mellan två tal är noll, dvs att de ligger bredvid varandra är
då p0 = p. Sannolikheten att avståndet är 1
är p 1 = p(1-p). Sedan följer på samma sätt
p 2 = p(1-p)2, p3 = p(1-p)3
, p t = p(1-p)t. t är det längsta uppmätta
avståndet. Detta ger utrycket för Q som finns på sid 111
(Håkan använder symbolen V i stället för Q). Vi får
räkna ut Q och gå in i samma tabell som i Chi2-testet ovan för
att avgöra om Q verkar rimligt.
Kupongtest
Detta test kontrollerar att inte något tal dyker upp orimligt
sällan. Detta kontrolleras i någon mån även av Chi2-testet
men med det kan det vara svårt att upptäcka felet om alla utfall
utom ett sker med rimlig frekvens.
Kupongtestet är likt Gap-testet fast här är hinkarna
inte ett visst avstånd mellan två tal utan längden av
en sekvens innan alla möjliga utfall har skett. Sannolikheten för
en viss sekvenslängd ges av formeln längst ner på sid 111.
Slumptal som inte är rektangulärfördelade
Det går att simulera vilken fördelning som helst med hjälp
av en slumpgenerator som ger rektangulärfördelade slumptal.
Diskret fördelning
I en diskret fördelning är bara vissa bestämda utfall
tillåtna. Det är inte så svårt om alla utfall ska
vara lika sannolika heltal, här är ett program som simulerar
tärningskast, Dice.c
. Det löste vi enkelt eftersom det fanns en färdig funktion
random(int num) som gör arbetet åt oss.
Lite klurigare blir det om de olika utfallen inte ska ha samma sannolikhet.
Här kommer ett program där utfallet 1 har 60% sannolikhet, 2
har 30% sannolikhet och 3 10%, Discrete.c
. Instruktionen (float) rand()/RAND_MAX ger ett tal i intervallet
[0, 1[. Vi låter utfall 1 ske om talet är i intervallet [0,
0.6], utfall 2 omtalet är i intervallet [0.6, 0.9[ och annars utfall
3.
Normalfördelning
En normalfördelning ser ut som på sid 113 i kompendiet.
Normalfördelade utfall är tex längden av slumpmässigt
valda personer eller restiden mellan två punkter.
En normalfördelning med medelvärdet 0 och standardavvikelsen
1, N(0, 1) får vi genom att slumpa två rektangulärfördelade
slumptal, r1 och r2 i intervallet ]0, 1[ och sedan beräkna det normalfördelade
slumptalet n1 enligt formeln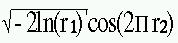 En normalfördelning n2 med medelvärdet
µ och standardavvikelsen σ kan vi erhålla genom att beräkna
n 2 = µ + σ n1.
En normalfördelning n2 med medelvärdet
µ och standardavvikelsen σ kan vi erhålla genom att beräkna
n 2 = µ + σ n1.
Poissonfördelning
Om vi vet hur många händelser det i genomsnitt inträffar
per tidsenhet beskriver poissonfördelningen sannolikheten att ett visst
antal händelser inträffar under en viss tidsperiod. Om det till
exempel komer in tio kunder i timmen till ett bankkontor (dvs i genomsnitt
λ = 10/60 = 1/6 kund per minut) är sannolikheten att det under en minut
kommer 1, 2, osv kunder = P(1/6), x = 1, 2, ... Formeln för poissonfördelning
finns på sid 115 i kompendiet.
Vi kan skapa ett poissonfördelat slumptal på följande
sätt:
- Generera ett rektangulärfördelat slumptal, r, i intervallet
]0, 1[.
- Initiera två variabler, antal = 0 och tid = 0.
- Beräkna variabeln intervall = -ln(r)/λ.
- Öka tid med intervall.
- Öka antal med 1.
- Utför punkt två till fem så länge tid < 1.
- Det poissonfördelade slumptalet är antal - 1.
Här är ett program som genererar tio poissonfördelade utfall
av hur många kunder det kommer in till banken under en minut i exemplet
ovan, Poisson.c
.
Exponentialfördelning
Om antalet händelser under en viss tid är poissonfördelat
(som i exemplet ovan) är tiden mellan dem exponentialfördelad.
Ett exponentialfördelat slumptal, e, kan beräknas som e = -λln(r).
r är även här ett rektangulärfördelat slumptal i
intervallet ]0, 1[ och λ är medelvärdet för de exponentialfördelade
slumptalen.
Här är ett program som genererar exponentialfördelade slumptal
som beskriver tiden mellan två kunder (i minuter) i exemplet ovan,
Exponent.c
. Eftersom det kommer 10 kunder/timme är medelvärdet 6 minuter
mellan två kunder.
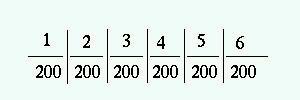 Nej, knappast. Kan det vara så att om vi kastar tillräckligt
många gånger är det säkert att resultaten blir så
jämnt fördelade? Nej, inte det heller för då skulle
resultatet av det sista kastet vara förutbestämt ("slumpen har
inget minne"). Ett troligare resultat av 1200 kast med tärningen
är nog detta:
Nej, knappast. Kan det vara så att om vi kastar tillräckligt
många gånger är det säkert att resultaten blir så
jämnt fördelade? Nej, inte det heller för då skulle
resultatet av det sista kastet vara förutbestämt ("slumpen har
inget minne"). Ett troligare resultat av 1200 kast med tärningen
är nog detta: 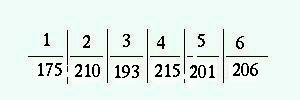 Innebär det att alla resultat är lika sannolika? Det är
den frågan som besvaras av Chi2-testet. Varje kast med tärningen
resulterar i ett utfall (1-6). Betrakta varje utfall som en hink. När
alla kast har gjorts vet vi hur många utfall som hamnade i varje
hink. Sedan beräknar vi summan Q av kvadraten på skillnaden
mellan förväntat och verkligt utfall dividerat med förväntat
utfall,
Innebär det att alla resultat är lika sannolika? Det är
den frågan som besvaras av Chi2-testet. Varje kast med tärningen
resulterar i ett utfall (1-6). Betrakta varje utfall som en hink. När
alla kast har gjorts vet vi hur många utfall som hamnade i varje
hink. Sedan beräknar vi summan Q av kvadraten på skillnaden
mellan förväntat och verkligt utfall dividerat med förväntat
utfall, 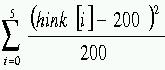 , se sid 108. I vårt exempel blir Q = 5,18. Nu är det dags
för en titt i tabellen på sid 109. Raderna representerar antalet
frihetsgrader , dvs antalet hinkar -1, 5 i vårt exempel.
Kolumnerna anger hur många procents sannolikhet det är att Q
ska vara mindre än ett visst värde. Med fem frihetsgrader är
det sannolikheten 75% att Q är mindre än 6,626 och 50% sannolikhet
att Q är större än 4,351. Det finns ingen anledning att misstänka
att tärningen/slumptalsgeneratorn är felaktig. Det är vad
ett Chi2-test kan säga oss.
, se sid 108. I vårt exempel blir Q = 5,18. Nu är det dags
för en titt i tabellen på sid 109. Raderna representerar antalet
frihetsgrader , dvs antalet hinkar -1, 5 i vårt exempel.
Kolumnerna anger hur många procents sannolikhet det är att Q
ska vara mindre än ett visst värde. Med fem frihetsgrader är
det sannolikheten 75% att Q är mindre än 6,626 och 50% sannolikhet
att Q är större än 4,351. Det finns ingen anledning att misstänka
att tärningen/slumptalsgeneratorn är felaktig. Det är vad
ett Chi2-test kan säga oss.