Träd

Definition

• Två noder som har samma förälder kallas syskon (tex är I och J syskon i fig 5.1).
• Alla noder från en viss nod och uppåt kallas nodens förfäder (i fig 5.1 är G, C och A förfäder till G).
• Alla noder från en viss nod och nedåt kallas nodens avkomma (i fig 5.1 är G, I och J avkomma till G).
• Ett träds höjd är antal noder (inklusive roten) på längsta vägen från roten till ett löv. Trädet i figuren har höjden 4.
• En nods djup är antalet noder (inklusive roten) som passeras på väg från noden till roten. Noden J i figuren har djupet 3.

Ordnat träd

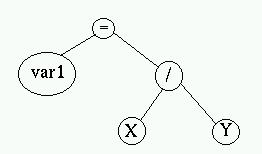
Trädet i bilden ovan beskriver instruktionen var1 = X / Y; . Trädet måste vara ordnat eftersom det har betydelse i vilken ordning noderna läses (var1 = Y / X; betyder något helt annat).

Binärt träd

Binärt sökträd

Notera att  definitionen ovan inte tillåter dubletter, dvs det får inte finnas två likadana nycklar. Definitionen skulle kunna utökas till att tillåta likadana nycklar men det är oftast bättre att lagra element med samma nyckel i samma nod (till exempel i en lista).

Operationer på binära sökträd

• struct Node* search(KeyElement key)

precondition: Ingen
postcondition: Trädet är oförändrat.
returnerar: En pekare till noden med den sökta nyckeln om den fanns i trädet, annars NULL.
 
• struct Node* min()

precondition: Ingen
postcondition: Trädet är oförändrat.
returnerar: En pekare till noden med den minsta nyckeln eller NULL om trädet är tomt.
 
• struct Node* max()

precondition: Ingen
postcondition: Trädet är oförändrat.
returnerar: En pekare till noden med den största nyckeln eller NULL om trädet är tomt.
 
• int insert(KeyElement key)

precondition: Ingen
postcondition: Trädet oförändrat förutom att en nod med nyckeln key är inlagd. Trädet är fortfarande ett binärt sökträd.
returnerar: 0 om operationen lyckas (nyckeln key fanns inte i trädet) annars -1 (nyckeln key fanns redan i trädet).
 
• int remove(KeyElement key)

precondition: Ingen
postcondition: Trädet oförändrat förutom att en noden med nyckeln key är borttagen. Trädet är fortfarande ett binärt sökträd.
returnerar: 0 om operationen lyckas (nyckeln key fanns i trädet) annars -1 (nyckeln key fanns inte i trädet).

• void beforeFirst()

precondition: ingen
postcondition: trädet oförändrat
Placerar cursorn först i trädet.
 
• struct Node* next()

precondition: ingen
postcondition: trädet oförändrat
returnerar: Elementet i trädet efter det som senast returnerades.
 
• bool hasNext()

precondition: ingen
postcondition: trädet oförändrat
returnerar: true om det finns fler element i trädet, annars false.

Implementation av binärt sökträd

Nu deklarerar vi själva trädet:
struct Node* root = NULL;
Det enda vi behöver hålla reda på är roten. Den innehåller pekare till sina barn som har pekare till sina barn osv.

Så över till operationerna. Vi börjar med min() som ska returnera noden med minst nyckel. Den hittar vi genom att hela tiden gå nedåt till vänster (vänster barn är alltid mindre än aktuell nod). Vi returnerar noden längst ner till vänster. min() anropar bara en privat metod _min(struct Node* n) som gör hela jobbet. Det är därför att _min() kommer att användas av andra publika metoder som inte ska söka från roten. Däremot ska användaren av vårat bibliotek inte behöva hålla reda på trädets rot, så vi kan inte låta min() ta en nod som inparemeter.
struct Node* min() {
  return _min(root);
}

struct Node* _min(struct Node* n) {
  struct Node* min = n;
  while (min->leftChild != NULL) {
    min = min->leftChild;
  }
  return min;
}
Sedan tar vi max(), den fungerar precis som min() men vi går år höger hela tiden.
struct Node* max() {
  return _max(root);
}

struct Node* _max(struct Node* n) {
  struct Node* max = n;
  while (max->rightChild  != NULL) {
    max = max->rightChild;
  }
  return max;
}
Notera hur lätt det är att hitta minsta respektive största elementet. Hade datastrukturen varit osorterad skulle det varit nödvändigt att läsa alla element för att veta vilket som var minst eller störst.

Så var det dags för traverseringen. Det finns tre olika sätt att traversera ett binärt träd:

1. Inorder Besök först en nods vänstra barn, sedan noden själv och sist nodens högra barn.
2. Preorder Besök först noden själv, sedan dess vänstra barn och sist dess högra barn.
3. Postorder Besök först nodens vänstra barn, sedan dess högra barn och sist noden själv.

Nu tittar vi på next(). Den ska hitta noden som är närmast större än cursor. Eftersom det inorder traversering ska vi till höger barn efter att ha varit i aktuell nod. Detta görs med raderna
  if (cursor->rightChild != NULL) {
    next = cursor->rightChild;
Nu är vi nere i det högra barnet. Den minsta noden under det är dess nedersta vänstra avkomma, den hittar vi med raden
    next = _min(next);
Så var det klart. Det andra fallet är om aktuell nod inte har något högerbarn. Då måste vi upp till dess förälder i stället.
  } else {
    next = cursor->parent;
Om vi kom från ett vänsterbarn upp till föräldern har vi hittat nästa nod eftersom inorder betyder att efter vänstra barnet kommer föräldern. Om vi däremot kom från ett högerbarn hade vi redan varit i föräldern. Vi måste då vidare upp tills vi når en nivå där vi kom från ett vänsterbarn.
    struct Node* ch = cursor;
    while (next != NULL && ch == next->rightChild) {
      ch = next;
      next = next->parent;
    }
  }
Kontrollen next != NULL i while-loopen beror på att om vi redan besökt alla noder kommer vi att fortsätta hela vägen upp till roten vars parent är NULL. Nu har vi hittat nästa nod. Vi returnerar cursor och uppdaterar den till att peka på nästa nod.
  struct Node* current = cursor;
  cursor = next;
  return current;
Pust! Nu är vi klara med next().

Lyckligtvis är hasNext() betydligt enklare. Traverseringen är slut om cursor är NULL. Vi har då gått igenom hela trädet och kommit till rotens förälder, se next() .
bool hasNext() {
  return cursor != NULL;
}

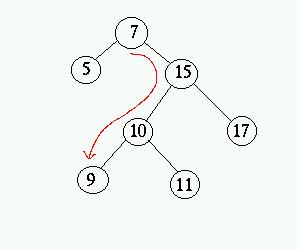
Sökning efter ett visst element sker genom att alltid jämföra värdet i aktuell nod med det sökta elementet. Om de är lika har vi hittat den sökta noden, om det sökta elementet är mindre än det i aktuell nod går vi ned till det vänstra barnet och om det sökta elementet är större går vi ned åt höger. Bilden nedan visar den väg search() tar för att hitta noden med nyckeln 9.

insert() fungerar på nästan samma sätt som search(). Först söker den efter en nod med den nyckeln som ska läggas in. Hittas en sådan nod kan den nya noden inte läggas in eftersom det inte får finnas dubletter. Om det inte finns någon nod med den nya nyckeln läggs den nya noden in där sökningen returnerade NULL. Detta innebär att trädet fortfarande är ett binärt sökträd eftersom vi sökt ut positionen enligt reglerna för att bonärt sökträd. 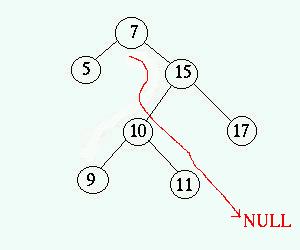Notera att detta innebär att nya noder alltid blir löv. I bilden nedan visas en sökning efter en nod med nyckeln 12. En sådan finns inte vilket innebär att en ny nod med nyckeln 12 kan läggas in där sökningen returnerar NULL.

Lägg märke till hur mycket mer kod det är i operationen insert() än i search(). Det beror till stor del på att insert() är iterativ medans search() är rekursiv.

Slutligen återstår operationen remove() som dessvärre är den krångligast av alla. Först söker vi efter en nod med den nyckel som ska tas bort (på samma sätt som i search() ). Därefter sönderfaller algoritmen i tre olika fall:

1. Noden som ska tas bort är ett löv

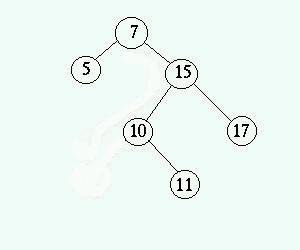
Det är bara att ta bort noden och sätta förälderns pekare som tidigare pekade ut noden till NULL.
2. Noden som ska tas bort har ett barn

Förälderns pekare som tidigare pekade ut noden ändras till att peka på barnet varefter noden tas bort. Bilderna nedan visar hur noden 10 tas bort ur trädet.

 
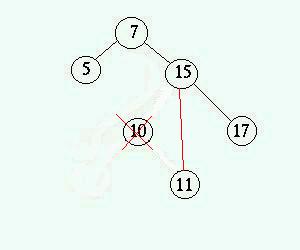
3. Noden som ska tas bort har två barn
• Tilldela noden värdet av den minsta noden i dess högra subträd. Denna är den med närmast högre värde än den som ska tas bort. Högre värde eftersom den ligger nedåt till höger, närmast högre eftersom det är den minsta i det högra subträdet. På detta vis är noderna fortfarande rätt sorterade.
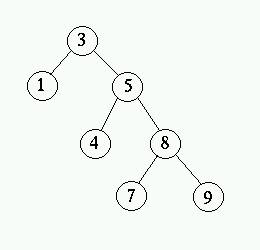
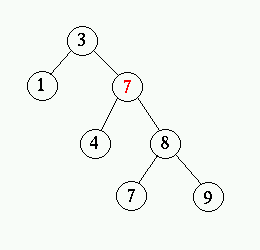
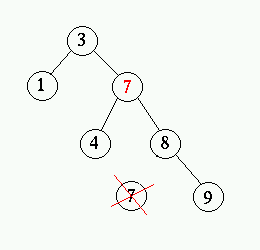
• Tag bort den nod vars värde kopierades (den minsta till höger). Detta måste vara enligt fall ett eller två eftersom den inte kan ha något vänsterbarn (detta skulle varit ännu mindre). Bilderna nedan visar hur noden 5 tas bort.

Prestanda för implementationen

1. Vad gäller traverseringen finns det flera alternativa implementationer. Olika datastrukturer, till exempel en länkad lista, där elementen är sorterade kan byggas redan vid beforeFirst(). Sedan hämtas elementen vid traversering ur den. Detta gör traverseringen klart långsammare medans många andra operationer blir lite snabbare på grund av att vi slipper pekaren parent.
2. Vi kan konstatera att exekveringshastigheten av så gott som alla operationer är proportionell mot djupet av den nod som hanteras. Detta innebär att worst case är proportionell mot det nedersta lövets djup. Kan vi då veta vilken höjd ett visst träd har? Svaret är att höjden är helt beroende av i vilken ordning noderna läggs in. Bilderna nedan visar två träd med exakt samma noder men noderna är inlagda i olika ordning.


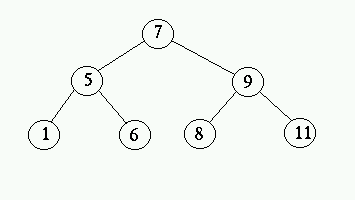
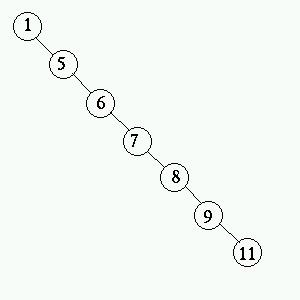
Trädet till vänster kallas balancerat . Trädet till höger har degenererat till en länkad lista. Detta är de två extremfallen, det är lätt att inse att de har ganska olika prestanda. Den nedersta noden i det högra trädet har djupet 6 medans den i det vänstra har djupet 2. Finns det då något genomsnitt? Mer generellt har ett balancerat träd ett djup som är största heltalet mindre än log₂ n, där n är antalet noder i trädet. Ett träd av typen i den högra bilden ovan har djupet n-1. Detta innebär att trädet till vänster är O(log n) medans trädet till höger är O(n), en väsentlig skillnad. Det går att visa att ett träd i genomsnitt har djupet 1,38log n, dvs det är O(log n).

Det finns olika strategier att stuva om noderna i träd när nya noder läggs in så att träden ska vara så nära balancerade som möjligt. Några exempel är AVL-träd, röd-svarta träd och AA-träd. Gemensamt för dem alla är att insert() och remove() blir lite långsammare eftersom noderna måste stuvas om. Eftersom de är väldigt nära balancerade blir djupet ungefär log n i stället för 1,38log n, dvs ungefär 25% snabbare.