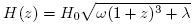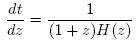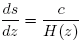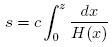How Far Out in the Universe Can We See?

by Harald Lang

    Calculations

Space is expanding, and the rate of expansion is measured by the Hubble-parameter H(z). It varies in time, i.e., it takes different values at different points in time. The starting point for the compu­tations is this very function. In a flat universe it is given by

where ω = the density of matter, about = 0.27, λ = cosmological constant, about = 0.73, and 1/H0 about = 13'775 million years.

The dimension of H0 is 1/time. If H0 is 71 km per sec. per mega-parsec, it corre­sponds to 1/H0 = 978/71 billion years, since 1 mega-parsec per year corres­ponds to 978 billion km per second. We take this formula as a starting point; it comes from the cosmological model.

Let us now determine the relation between time t (measured from today backwards in time) and the red-shift z. Consider two points in time, t+dt and t with a small time spell dt in between, whose corresponding red-shifts are z+dz and z. We imagine a photon that is emitted at time t+dt and travels towards us. Shortly thereafter, at time t, space has ex­panded somewhat, more precisely by the factor (1+H(z)dt), according to the very definition of H(z). As a consequence, also the wavelength of the photon has ex­panded by the same factor. Now the photon continues its travel towards us, and under the remaining time the wavelength is stretched out by the factor (1+z). When the photon reaches us, its wavelength has thus in total been multiplied by (1+H(z)dt)·(1+z). But, on the other hand, it is also clear that the wavelength has been multi­plied by (1+z+dz). Hence, we have the equality

(1+H(z)dt)·(1+z) = (1+z+dz),

which gives dz = (1+z)·H(z)dt, or

We interpret the LHS as a derivative, and those who know the relationship between derivatives and integrals realize now that we get the relation "time expressed in red-shift" t=t(z) by integrating the above ex­pres­sion:

which can be computed to the formula in the main text.

In order to get the relation between the co-moving distance (the "distance now") and the red-shift z we multiply the equality dz = (1+z)·:H(z)dt above with the speed of light, c: c·dz = c·dt·(1+z)H(z). The distance between the two points in space where the photon was at the times t+dt and t was then, at that time, obviously c·dt, but now that distance has expanded by the factor (1+z), and is hence c·dt·(1+z) = ds. Here ds thus denotes the distance today between these two points in space. Hence we can write

c·dz = c·dt·(1+z)H(z) =ds·H(z), i.e.,

Again we interpret the LHS as a derivative: the derivative of the distance today w.r.t. the redshift, and we integrate in order to get s expressed in terms of z, s=s(z):

However, this time the integration must be performed numerically.

  
 

At least some of us are fascinated by the distances in space and time we encounter in the Universe. How old is the Universe? How far away is an object whose red-shift is 3.0, for example? How far out can we see, and how far out is it possible that we ever can see? I will somewhat address these issues in this article.

To begin with, it is important to specify which model we use for the calculations. I employ the Big Bang model (with a positive cosmological constant) that there is currently almost consensus about. Space expands; a distance which at an earlier point in time t was D units of length is today longer: D(1+z) units of length. The number z is called the "red-shift", since also photons (light) is stretched out by the same amount: light that had a wave­length of λ at time t has been red-shifted, and has today a wavelength of λ(1+z).

There is thus a unique correspondence between time t and red-shift z. It is easiest to count time backwards, so that "now" time is t=0 and corre­sponds to z=0, and time t="665 million years" is 665 million years ago and corre­sponds to z=0.05. It is often simpler, mathematically, to use z as a parameter rather than time. For example, we can talk about how things were in the Universe at "time" z=10. When we see a distant galaxy, it is rather easy to determine its red-shift, so we can say that the light we see was emitted at "time" z.

Before we go on, I present the unfortunately some­what messy relation between time t and red-shift z:
Time t =

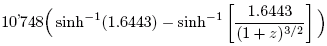
million years (Here I have used the currently estimated values of the parameters in the model; see the frame to the right.) This expression can be computed on a "scientific" pocket calculator; "sinh" stands for "hyperbolic sine", and we need its inverse. On my calculator, I first press "hyp" and then inverse sine. For small values on z, say z <0,05, it is easier to use the approximate formula

t = 13'774.6 z – 9'676.7 z2

So now we can compute when the light from a galaxy with z=0.05 was emitted, either with the more exact formula or the approximate. We see that it's about 665 million years ago. If we see a galaxy with z=5, we compute the time since its light was emitted to about 12.47 billion years ago, i.e., when the Universe was quite young. Indeed, we can also compute the age of the Universe; i.e., the time since the Big Bang: at that time z was i principle infinitely large, so its age is

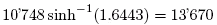
million years, i.e., 13.67 billion years.

Distances

The concept of distance in an expanding Universe is a bit slippery. What should one mean? Assume that we look at a galaxy with z=1, i.e., the light we see was emitted about 7.73 billion years ago. How far away is that galaxy today (if it still exists?) Not 7.73 billion light years away, since while its light has traveled towards us, space has expanded between it (the photon) and the galaxy behind it, so the galaxy is much farther away than the distance the photon has traveled. The "distance now" is often called the "co-moving distance", since it is the distance to the galaxy if it follows the general expansion of space. The formula for the co-moving distance is an integral that can not be expressed in terms of elementary functions, but it can be computed numerically (see the frame to the right.) One finds that the galaxy with z=1 is now 10.82 billion light years away. A galaxy with z=2 is 17.11 billion light years away. The distance in light years can hence exceed the age of the Universe (in years.) What the number means is this: Assume that the galaxy emits a photon towards us today, and that the expansion of the Universe were somehow halted. Then it would take 17.11 billion years for the photon to reach us, i.e., we would see it 17.11 billion years from now.

How far out can we see? We can not see farther out than z = 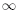(infinite,) which corresponds to photons emitted soon after the Big Bang. If we compute the integral for this value of z we get s=47.5 billion light years. Objects farther out that this can not currently be seen by us, and by the General Relativity Theory, we can not have any at all contact with them. "Our" Universe today is a ball with us in the center and a radius of 47.5 billion light years.

How far will we ever be able to see? Can we (in principle) see an object which currently resides, say, 70 billion light years away, if we wait long enough? The answer is No!. The Universe we ever can come in contact with has a radius (currently) of about 63 billion light years! We can compute that from the integral formula by integrating from z=-1 to z = .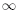

The value z=-1 represents time when the expansion grows to infinity, so we are looking into the infinite future. This gives s=63 billion light years, about, and is hence as far out as we ever has a possibility to see.

This is due entirely to the "cosmological constant", or "dark energy", as it is sometimes called. Note that this is something entirely different from the "dark matter" that also is regarded to exist. But the fact that the cosmological constant exists,—i.e., is positive and not zero—has the consequence that the "Universe for Us" is finite, which it would not be otherwise.

In my opinion the introduction of the cosmological constant has profound philosofical consequences. Some years ago, the general assumption was that it was equal to zero, and it was then meaningful to speculate about the overall structure of the Universe, since we could in principle come in contact with all its parts, if we just waited long enough. But with a positive cosmological constant all such speculations become nonsensical, in a way. If the model describes reality correct, then it is for ever impossible to even imagine that we could verify any at all hypothesis about how the Universe behaves outside a radius of 63 billion light years. Outside of this radius the Universe is non-existent for us.