Most of my papers deal with finite abstract simplicial complexes.
The emphasis is typically on homological and enumerative
properties of such complexes. Quite a few of my results admit
interpretations in terms of geometric cell complexes, e.g., via
Robin Forman's discrete Morse theory. Yet, most of my proof
methods are not geometric or topological in nature.
- On the Topology of Simplicial Complexes Related to 3-connected and Hamiltonian Graphs
Journal of Combinatorial Theory, Series A 104 (2003), 169-199. Available in pdf format.
If you are unhappy with this format, send me a note.
Show abstract
Hide abstract
Using techniques from the discrete Morse theory developed by Robin
Forman, I obtain information about the homology and homotopy type
of some graph complexes. More precisely, I prove that the
simplicial complex of not 3-connected graphs on n vertices
is homotopy equivalent to a wedge of
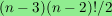 spheres of dimension
spheres of dimension
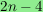 ,
thereby verifying a conjecture by
E. Babson, A. Björner, S. Linusson, J. Shareshian, and
V. Welker. I also examine the complex of non-Hamiltonian graphs on
n vertices, which turns out to be closely related (but not
homotopy equivalent) to the complex of not 2-connected graphs. A
complete description of the homotopy type of non-Hamiltonian graphs
remains to be given.
,
thereby verifying a conjecture by
E. Babson, A. Björner, S. Linusson, J. Shareshian, and
V. Welker. I also examine the complex of non-Hamiltonian graphs on
n vertices, which turns out to be closely related (but not
homotopy equivalent) to the complex of not 2-connected graphs. A
complete description of the homotopy type of non-Hamiltonian graphs
remains to be given.
- Optimal Decision Trees on Simplicial Complexes
Electronic Journal of Combinatorics 12(1) (2005), #R3. Direct
link to journal.
Show abstract
Hide abstract
I consider decision trees on simplicial complexes and the
related concept of evasiveness. In a famous paper of Kahn, Saks, and
Sturtevant, it was observed that a complex is evasive
unless it is contractible. Using discrete Morse theory, R. Forman
generalized their observation and showed that a decision tree
transforms a simplicial complex into a smaller homotopy equivalent
CW complex with one cell for each evasive set. Under certain
favorable circumstances, a simplicial complex admits an ``optimal''
decision tree such that the evasive sets are enumerated by the
reduced Betti numbers of the complex; we may hence read off the
homology directly from the tree. I provide a recursive definition
of the class of such complexes and generalize in a direction
inspired by the recursive definition of shellability due to
Provan-Billera. I also provide explicit optimal decision trees for a
long list of well-known complexes.
- Simplicial Complexes of Graphs and Hypergraphs with a Bounded Covering Number
SIAM Journal of Discrete Mathematics 19 (2005), no. 3, 633-650.
Available in pdf
format.
If you are unhappy with this format, send me a note.
Show abstract
Hide abstract
For
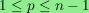 ,
define
,
define
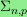 as the simplicial complex of graphs (identified with their edge
sets) on the vertex set
as the simplicial complex of graphs (identified with their edge
sets) on the vertex set
 with covering
number at most p (equivalently, with independence number
at least
with covering
number at most p (equivalently, with independence number
at least
 .
For
.
For
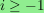 ,
I show that the rank
of the i-th homology group of
,
I show that the rank
of the i-th homology group of
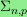 is a linear combination, with
coefficients being polynomials in n, of the ranks of the
i-th homology groups of
is a linear combination, with
coefficients being polynomials in n, of the ranks of the
i-th homology groups of
 .
My proof takes place in a more general
setting where I consider complexes of hypergraphs.
In addition, I show that the
.
My proof takes place in a more general
setting where I consider complexes of hypergraphs.
In addition, I show that the
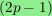 -skeleton of
-skeleton of
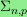 is
vertex-decomposable, which implies that
is
vertex-decomposable, which implies that
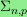 is
is
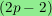 -connected.
For
-connected.
For
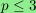 ,
I give a complete description of the
homology groups of
,
I give a complete description of the
homology groups of
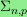 .
.
- The Topology of the Space of Matrices of
Barvinok Rank Two
Joint work with Axel Hultman. Beiträge zur Algebra und
Geometrie, to appear.
Available in pdf format.
If you are unhappy with this format, send me a note.
Show abstract
Hide abstract
The Barvinok rank of a
 matrix is the minimum number of
points in
matrix is the minimum number of
points in
 such that the tropical convex hull of the
points contains all columns of the matrix. The concept originated in
work by Barvinok and others on the travelling salesman problem.
Our object of study is the space of real
such that the tropical convex hull of the
points contains all columns of the matrix. The concept originated in
work by Barvinok and others on the travelling salesman problem.
Our object of study is the space of real
 matrices of Barvinok rank two. Let
matrices of Barvinok rank two. Let
 denote this space modulo rescaling and translation.
We show that
denote this space modulo rescaling and translation.
We show that
 is a manifold, thereby settling a
conjecture due to Develin. In fact,
is a manifold, thereby settling a
conjecture due to Develin. In fact,
 is homeomorphic to the
quotient of the product of spheres
is homeomorphic to the
quotient of the product of spheres
 under
the involution which sends each point to its antipode simultaneously in both
components.
In addition, using discrete Morse theory, we compute the integral
homology of
under
the involution which sends each point to its antipode simultaneously in both
components.
In addition, using discrete Morse theory, we compute the integral
homology of
 .
Assuming
d ≥ n,
for odd d the homology
turns out to be
isomorphic to that of
.
Assuming
d ≥ n,
for odd d the homology
turns out to be
isomorphic to that of
 .
This is true also for even d up to degree
.
This is true also for even d up to degree
 ,
but the two cases differ from degree
,
but the two cases differ from degree
 and up.
The homology computation straightforwardly extends to more general
complexes of the form
and up.
The homology computation straightforwardly extends to more general
complexes of the form
/\mathbb{Z}_2&bg=90EE90&s=0) ,
where X is a finite cell
complex of dimension at most
,
where X is a finite cell
complex of dimension at most
 admitting a free
admitting a free
 -action.
-action.
- A Refinement of
Amplitude Homology and a Generalization of Discrete Morse
Theory
Submitted, 2011.
Available in pdf
format.
If you are unhappy with this format, send me a note.
Show abstract
Hide abstract
Let n ≥ 2. A chain complex with boundary map δ has
the property that δ = 0. Kapranov introduced the
concept of an n-complex, in which we instead have
that δn = 0. Kapranov also generalized the
concept of
homology to n-complexes, introducing n-1 generalized
homology groups, where the kth group is defined as the
quotient ker δk / im
δn-k.
One goal of the present paper is to introduce n-1 new
groups that I refer to as train groups.
The train groups are closely related to
generalized homology groups; there exists a filtration of each
generalized homology group such that each quotient arising from
the filtration is a direct sum of train groups.
In particular, one may view the train groups as refinements of
the generalized homology groups.
Another goal is to generalize the algebraic version of Forman's
discrete Morse theory to n-complexes. I will then make use
of the theory of generalized homotopies introduced by Kapranov and
further developed by Kassel and Wambst and by Dubois-Violette.
- Hom Complexes of Set Systems
Preprint, revised version 2012.
Available in pdf
format.
If you are unhappy with this format, send me a note.
Show abstract
Hide abstract
A set system is a pair S =
(V(S),Δ(S)), where Δ(S)
is a family of subsets of the set V(S). We refer to
the members of Δ(S) as the stable sets of
S. A homomorphism between
two set systems S and T is a map f :
V(S) \rightarrow V(T)
such that the preimage under f of every stable set
of T is a stable set of S.
Inspired by a recent generalization due to Engström
of Lovász' Hom complex construction,
I show how to associate a cell complex
Hom(S,T) to any two
set systems S and T.
The main goal is to examine partitionability of set systems.
Specifically, a partition of a set system S is a
partition of V(S) into stable sets. A transversal of
S is a subset of V(S) such that no two
elements in the subset belong to a common stable set. We say that
S is partitionable if the size of a minimal partition
coincides with the size of a maximal transversal.
I show that the topology of the cell complex
Hom(S,T) is related to
the partitionability of T. Loosely speaking, if
T is partitionable, then the homology
of Hom(S,T) must have certain properties.
This yields an obstruction theory for partitionability.
The motivating example is the case that the stable sets of
T are the closed intervals in a simplicial complex.
Being partitionable is then equivalent to admitting a
partition into intervals, each containing a maximal face.
-
Simplicial Complexes of Subgraphs of a Graph on at most Six Vertices
Manuscript.
Available in pdf
format.
If you are unhappy with this format, send me a note.
Show abstract
Hide abstract
For any fixed graph G on the vertex set V, we may
define a monotone graph property
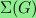 consisting of all
graphs on V that are contained in a graph isomorphic to
G. This document contains a list of all nontrivial complexes
of this kind on a vertex set of size
4, 5, or 6.
More precisely, for each nontrivial isomorphism
class
consisting of all
graphs on V that are contained in a graph isomorphic to
G. This document contains a list of all nontrivial complexes
of this kind on a vertex set of size
4, 5, or 6.
More precisely, for each nontrivial isomorphism
class
 of graphs, I have computed the homology of the
associated complex
of graphs, I have computed the homology of the
associated complex
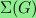 using the computer program homology written by Frank Heckenbach.
using the computer program homology written by Frank Heckenbach.
- Five-Torsion in the Homology of the Complex on 14 Vertices
Journal of Algebraic Combinatorics 29 (2009), no. 1, 81-90.
Available in pdf format.
If you are unhappy with this format, send me a note.
Show abstract
Hide abstract
J. L. Andersen proved that
there is 5-torsion in the bottom nonvanishing homology group of
the simplicial complex of graphs of degree at
most two on seven vertices. I use this result to demonstrate that
there is 5-torsion
also in the bottom nonvanishing homology group of the matching
complex
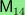 on 14 vertices.
Combining our observation with results due to Bouc
and to Shareshian and Wachs, I
conclude that the case
on 14 vertices.
Combining our observation with results due to Bouc
and to Shareshian and Wachs, I
conclude that the case
 is exceptional; for all other n,
the torsion subgroup of the bottom nonvanishing homology group
has exponent three or is zero.
The possibility remains that there is other torsion than
3-torsion in higher-degree homology groups of
is exceptional; for all other n,
the torsion subgroup of the bottom nonvanishing homology group
has exponent three or is zero.
The possibility remains that there is other torsion than
3-torsion in higher-degree homology groups of
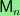 when
when
 and
and
 .
.
- Exact Sequences for the Homology of the Matching Complex
Journal of Combinatorial Theory, Series A 115 (2008),
no. 8, 1504-1526.
Available in pdf format.
If you are unhappy with this format, send me a note.
Show abstract
Hide abstract
Building on work by Bouc and by Shareshian and Wachs, I provide a
toolbox of long exact
sequences for the reduced simplicial homology of the matching
complex
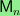 , which
is the simplicial complex of
matchings in the complete graph
, which
is the simplicial complex of
matchings in the complete graph
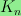 .
Combining these sequences in
different ways, I prove several results about the
3-torsion part of the homology of
.
Combining these sequences in
different ways, I prove several results about the
3-torsion part of the homology of
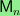 .
First, I demonstrate that there is nonvanishing
3-torsion in
.
First, I demonstrate that there is nonvanishing
3-torsion in
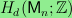 whenever
whenever
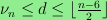 , where
, where
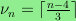 .
By a theorem due to Bouc and to Shareshian and Wachs,
.
By a theorem due to Bouc and to Shareshian and Wachs,
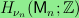 is a
nontrivial elementary 3-group for almost all n and the
bottom nonvanishing homology group of
is a
nontrivial elementary 3-group for almost all n and the
bottom nonvanishing homology group of
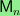 for all
for all
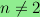 .
Second, I prove that
.
Second, I prove that
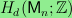 is a
nontrivial
3-group whenever
is a
nontrivial
3-group whenever
 .
Third, for each
.
Third, for each
 , I show
that there is a polynomial
, I show
that there is a polynomial
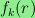 of
degree 3k such
that the dimension of
of
degree 3k such
that the dimension of
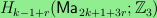 ,
viewed as a vector space
over
,
viewed as a vector space
over
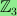 ,
is at most
,
is at most
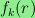 for all
for all
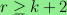 .
.
- On the 3-Torsion Part of the Homology of the Chessboard Complex
Annals of Combinatorics 14 (2010), no. 4, 487-505.
Available in pdf format.
If you are unhappy with this format, send me a note.
Show abstract
Hide abstract
Let m ≤ n.
I prove various results about
the chessboard complex
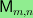 , which is the simplicial complex of
matchings in the complete bipartite graph
, which is the simplicial complex of
matchings in the complete bipartite graph
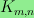 .
First, I demonstrate that there is nonvanishing
3-torsion in
.
First, I demonstrate that there is nonvanishing
3-torsion in
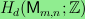 whenever
whenever
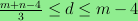 and
whenever
and
whenever
 and
and
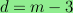 .
Combining this result with theorems due to
Friedman and Hanlon and to Shareshian and Wachs,
I characterize all triples
.
Combining this result with theorems due to
Friedman and Hanlon and to Shareshian and Wachs,
I characterize all triples
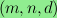 satisfying
satisfying
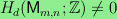 .
Second, for each
.
Second, for each
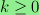 ,
I show that there is a polynomial
,
I show that there is a polynomial
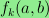 of degree 3k such that
the dimension of
of degree 3k such that
the dimension of
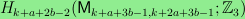 ,
viewed as a vector space over
,
viewed as a vector space over
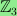 ,
is at most
,
is at most
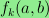 for all
for all
 and
and
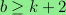 .
In addition, I give the first
computer-free proof that
.
In addition, I give the first
computer-free proof that
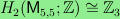 . Several proofs are based on a new long
exact sequence relating the homology of a certain subcomplex of
. Several proofs are based on a new long
exact sequence relating the homology of a certain subcomplex of
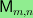 to the homology of
to the homology of
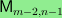 and
and
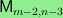 .
.
- More Torsion in the Homology of the
Matching Complex
Experimental Mathematics 19 (2010), no. 3, 363-383.
Available in pdf format.
If you are unhappy with this format, send me a note.
Source code in C used to generate the chain
complexes under consideration in the paper.
Show abstract
Hide abstract
Using computers, I analyze the integral homology of the matching
complex
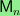 ,
which is the simplicial complex of matchings in
the complete graph on n vertices. Our main result is the
detection of p-torsion in the homology for p in
{5,7,11,13}. Specifically, I show that there is nonvanishing
5-torsion in the homology of
,
which is the simplicial complex of matchings in
the complete graph on n vertices. Our main result is the
detection of p-torsion in the homology for p in
{5,7,11,13}. Specifically, I show that there is nonvanishing
5-torsion in the homology of
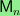 for n ≥ 18 and for n in {14,16}.
The only previously known value was n = 14, and
in this particular case I have a new computer-free proof.
Moreover, I show that there is 7-torsion in the homology of
for n ≥ 18 and for n in {14,16}.
The only previously known value was n = 14, and
in this particular case I have a new computer-free proof.
Moreover, I show that there is 7-torsion in the homology of
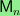 for all odd n between 23 and 41 and for n = 30.
In addition, there is 11-torsion in the homology of
for all odd n between 23 and 41 and for n = 30.
In addition, there is 11-torsion in the homology of
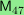 and 13-torsion in the homology of
and 13-torsion in the homology of
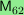 .
Finally, I compute the ranks of the 3- and 5-subgroups
of
.
Finally, I compute the ranks of the 3- and 5-subgroups
of
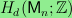 for 13 ≤ n ≤ 16; a complete
description of the homology already exists for n ≤ 12.
To prove our results, I use a representation-theoretic approach,
examining subcomplexes of the chain complex of
for 13 ≤ n ≤ 16; a complete
description of the homology already exists for n ≤ 12.
To prove our results, I use a representation-theoretic approach,
examining subcomplexes of the chain complex of
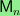 obtained by letting certain groups act on the chain complex.
obtained by letting certain groups act on the chain complex.
- 3-Torsion in the Homology of Complexes of Graphs of Bounded Degree
Preprint, revised version 2012.
Available in pdf format.
If you are unhappy with this format, send me a note.
Show abstract
Hide abstract
For
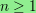 and δ ≥ 1, I examine the simplicial
complex of graphs on n vertices in which each vertex has degree
at most δ;
one identifies a given graph with its edge set and
admits one loop at each vertex.
and δ ≥ 1, I examine the simplicial
complex of graphs on n vertices in which each vertex has degree
at most δ;
one identifies a given graph with its edge set and
admits one loop at each vertex.
 yields the matching complex, and it is known that
there is 3-torsion in degree d of the homology of this complex
whenever
yields the matching complex, and it is known that
there is 3-torsion in degree d of the homology of this complex
whenever
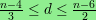 .
I establish similar bounds for δ ≥ 2.
Specifically,
there is 3-torsion in degree d whenever
.
I establish similar bounds for δ ≥ 2.
Specifically,
there is 3-torsion in degree d whenever
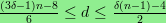 . The situation for other pairs
(d,n) remains unknown in general. To detect
torsion, I construct an explicit cycle z that is easily
seen to have the property that 3z is a boundary. Defining a
homomorphism that sends z to a non-boundary element in the
chain complex of a certain matching complex, I obtain that z
itself is a non-boundary. In particular, the homology class of
z has exponent 3.
. The situation for other pairs
(d,n) remains unknown in general. To detect
torsion, I construct an explicit cycle z that is easily
seen to have the property that 3z is a boundary. Defining a
homomorphism that sends z to a non-boundary element in the
chain complex of a certain matching complex, I obtain that z
itself is a non-boundary. In particular, the homology class of
z has exponent 3.
- Hard Squares with Negative Activity and Rhombus Tilings of the Plane
Electronic Journal of Combinatorics 13(1) (2006),
#R67. Direct link to journal.
Show abstract
Hide abstract
Let
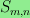 be the graph on the vertex set
be the graph on the vertex set
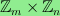 with an edge between
with an edge between
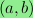 and
and
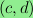 if
and only if either
if
and only if either
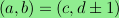 or
or
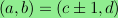 modulo
modulo
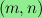 .
I consider the simplicial complex
.
I consider the simplicial complex
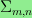 .
of independent sets in
.
of independent sets in
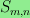 and present a formula for the
Euler characteristic of
and present a formula for the
Euler characteristic of
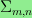 . In particular, I
show that the unreduced Euler characteristic of
. In particular, I
show that the unreduced Euler characteristic of
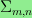 vanishes whenever m and n are relatively prime, thereby
settling a conjecture in statistical mechanics due to Fendley,
Schoutens and van Eerten. For general m and n, I relate
the Euler characteristic of
vanishes whenever m and n are relatively prime, thereby
settling a conjecture in statistical mechanics due to Fendley,
Schoutens and van Eerten. For general m and n, I relate
the Euler characteristic of
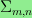 to
certain periodic rhombus tilings of the plane. Using this
correspondence, I settle
another conjecture due to Fendley et al., which states that all
roots of det
to
certain periodic rhombus tilings of the plane. Using this
correspondence, I settle
another conjecture due to Fendley et al., which states that all
roots of det
 are roots of unity,
where
are roots of unity,
where
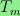 is a certain "transfer matrix"
associated to
is a certain "transfer matrix"
associated to
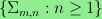 . In the language of statistical mechanics, the
reduced Euler characteristic of
. In the language of statistical mechanics, the
reduced Euler characteristic of
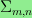 coincides with minus the partition function of the corresponding
hard square model with activity
coincides with minus the partition function of the corresponding
hard square model with activity
 .
.
- Certain Homology Cycles of the Independence Complex of Grids
Discrete and Computational Geometry 43 (2010), No. 4, 927-950.
Available in pdf
format.
If you are unhappy with this format, send me a note.
Show abstract
Hide abstract
Let G be an infinite graph such that the automorphism group of
G contains a subgroup
 with the property that
with the property that
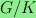 is finite.
I examine the homology of the independence complex
is finite.
I examine the homology of the independence complex
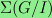 of
of
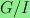 for subgroups I of K of full rank, focusing on
the case that G is the square, triangular, or hexagonal grid.
Specifically, I look for a certain kind of homology cycles referred
to as ``cross-cycles'', the rationale for the
terminology being that they
are fundamental cycles of the boundary
complex of some cross-polytope.
For the special cases just mentioned, I determine the set
for subgroups I of K of full rank, focusing on
the case that G is the square, triangular, or hexagonal grid.
Specifically, I look for a certain kind of homology cycles referred
to as ``cross-cycles'', the rationale for the
terminology being that they
are fundamental cycles of the boundary
complex of some cross-polytope.
For the special cases just mentioned, I determine the set
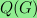 of rational numbers r such that there is a group I with the
property that
of rational numbers r such that there is a group I with the
property that
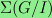 contains
cross-cycles of dimension exactly
contains
cross-cycles of dimension exactly
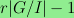 ;
;
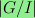 denotes the size of the vertex set of
denotes the size of the vertex set of
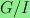 .
In each of the three cases,
.
In each of the three cases,
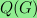 turns out to be an interval of
the form
turns out to be an interval of
the form
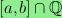 .
For example, for the square grid, one obtains the interval
.
For example, for the square grid, one obtains the interval
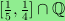 .
.
- Hard Squares with Negative Activity on Cylinders with Odd
Circumference
Electronic Journal of Combinatorics 16 (2009), no. 2, #R5.
Direct link to journal.
Show abstract
Hide abstract
Let 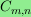 be the graph on the vertex set
be the graph on the vertex set
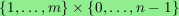 in which there is an edge between
in which there is an edge between
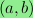 and
and
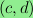 if and only if either
if and only if either
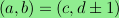 or
or
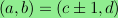 , where the second index is computed modulo n.
One may view
, where the second index is computed modulo n.
One may view
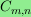 as a unit square grid on a
cylinder with circumference n units.
For odd n, I prove that the Euler characteristic of the
simplicial complex
as a unit square grid on a
cylinder with circumference n units.
For odd n, I prove that the Euler characteristic of the
simplicial complex
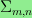 of independent sets in
of independent sets in
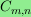 is either 2 or
is either 2 or
 ,
depending on whether or not
,
depending on whether or not
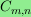 is divisble by 3. The proof relies heavily on
previous work due to Thapper,
who reduced the problem of computing the Euler characteristic of
is divisble by 3. The proof relies heavily on
previous work due to Thapper,
who reduced the problem of computing the Euler characteristic of
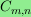 to that of analyzing a certain subfamily of sets
with attractive properties. The situation for even n remains
unclear.
In the language of statistical mechanics, the reduced Euler
characteristic of
to that of analyzing a certain subfamily of sets
with attractive properties. The situation for even n remains
unclear.
In the language of statistical mechanics, the reduced Euler
characteristic of
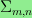 coincides with minus the
partition function of the corresponding hard square model
with activity
coincides with minus the
partition function of the corresponding hard square model
with activity
 .
.
-
Hard Squares on Grids With Diagonal Boundary Conditions
Manuscript, 2006. Available in pdf
format.
If you are unhappy with this format, send me a note.
Show abstract
Hide abstract
Let m and n be positive integers and let
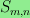 be
the graph obtained from the infinite square grid by identifying
two vertices
be
the graph obtained from the infinite square grid by identifying
two vertices
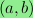 and
and
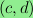 whenever
their difference
whenever
their difference
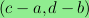 is an integer linear combination of the two vectors
is an integer linear combination of the two vectors
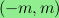 and
and
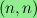 . I examine the
reduced Euler characteristic
. I examine the
reduced Euler characteristic
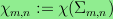 , where
, where
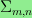 is the
simplicial complex of independent sets in
is the
simplicial complex of independent sets in
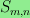 .
I prove that the behavior of
.
I prove that the behavior of
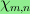 for fixed
m depends on the divisibility of m by
three. Specifically, if m is not
divisible by three, then
for fixed
m depends on the divisibility of m by
three. Specifically, if m is not
divisible by three, then
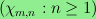 is periodic.
If m is divisible by three, then
is periodic.
If m is divisible by three, then
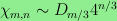 for large n, where
for large n, where
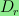 equals the number of
orbits under cyclic rotation of the set of all periodic sequences
of length 2r with r zeros and r ones.
The proof is based on results from the paper above.
equals the number of
orbits under cyclic rotation of the set of all periodic sequences
of length 2r with r zeros and r ones.
The proof is based on results from the paper above.
-
On the Topology of Independence Complexes of Triangle-Free Graphs
Preprint, 2010.
Available in pdf format.
If you are unhappy with this format, send me a note.
Show abstract
Hide abstract
The independence complex of a (finite) simple graph is the
abstract simplicial complex consisting of all independent vertex
sets in the graph.
I show that the possible homotopy types of independence complexes
of bipartite graphs are exactly those of suspensions of
simplicial complexes.
As a consequence, there exist bipartite graphs such that
the integral homology of the associated independence complex
is free. This answers a question by Engström.
The smallest such bipartite graph found so far has 16 vertices
and 30 edges.
- On the chromatic number of generalized stable Kneser graphs
Submitted, 2012. Available in pdf format.
If you are unhappy with this format, send me a note.
Show abstract
Hide abstract
For each integer triple (n, k, s) such that
k ≥ 2, s ≥ 2,
and n ≥ ks, define a graph in the following
manner. The vertex set consists of all k-subsets S
of Zn such that any two elements in
S are on circular distance at least s. Two
vertices form an edge if and only if they are disjoint. For the
special case s=2, we get Schrijver's stable Kneser
graph. The general construction is due to Meunier, who conjectured
that the chromatic number of the graph is
n-s(k-1). By a famous result
due to Schrijver, the conjecture is known to be true for s =
2. The main result of the present paper is that the conjecture is
true for s ≥ 4, provided n is sufficiently large
in terms of s and k. The proof techniques do not
apply to the case s=3, which remains nearly completely open.
- The exact chromatic number of the
convex segment disjointness graph
Preprint, 2011. Available in pdf format.
If you are unhappy with this format, send me a note.
Show abstract
Hide abstract
Given a set of n points in the plane in general and convex
position, let Ωn be the set of closed line
segments joining pairs of elements in the point set.
Let Dn be the graph whose vertex set is
Ωn,
where two line segments are adjacent if and only if they are
disjoint. In a more general setting,
Araujo, Dumitrescu, Hurtado, Noy, and Urrutia introduced the
problem of determining the chromatic number of
Dn.
Fabila-Monroy and Wood showed that a lower bound is given by
n - (2n + 1/4)1/2 + 1/2.
The main result of the present note is that the chromatic number
actually equals this lower bound (rounded up to the nearest
integer). The proof is constructive.
- Euler Trails and Trees in Directed Graphs
Thesis for the degree of licentiate, Stockholm University, September
1999. Available in pdf
format (title and abstract missing).
If you are unhappy with this format, send me a note.
(A licentiate degree is somewhat like a 50% Ph.D. degree; you spend
two years instead of four on graduate studies and research.)
Show abstract
Hide abstract
This thesis is about Euler trails and trees in digraphs.
In the first part of the thesis, I examine a matrix associated to
an Euler trail in an Eulerian digraph with all in- and out-degrees
equal to 2. This matrix was introduced by Macris and Pulé,
who proved that the determinant of the matrix counts the number of
Euler trails in the digraph.
In the second part, I consider further aspects of the theory of
directed spanning trees and Euler trails in digraphs. This theory
is closely related to Norman Biggs' algebraic potential theory on
graphs as well as to André Bouchet's theory of isotropic
systems.
Some (though maybe not the most interesting) parts of the thesis are
also published in
Mathematica Scandinavica 90 (2002).
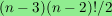 spheres of dimension
spheres of dimension
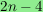 ,
thereby verifying a conjecture by
E. Babson, A. Björner, S. Linusson, J. Shareshian, and
V. Welker. I also examine the complex of non-Hamiltonian graphs on
n vertices, which turns out to be closely related (but not
homotopy equivalent) to the complex of not 2-connected graphs. A
complete description of the homotopy type of non-Hamiltonian graphs
remains to be given.
,
thereby verifying a conjecture by
E. Babson, A. Björner, S. Linusson, J. Shareshian, and
V. Welker. I also examine the complex of non-Hamiltonian graphs on
n vertices, which turns out to be closely related (but not
homotopy equivalent) to the complex of not 2-connected graphs. A
complete description of the homotopy type of non-Hamiltonian graphs
remains to be given.
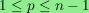 ,
define
,
define
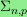 as the simplicial complex of graphs (identified with their edge
sets) on the vertex set
as the simplicial complex of graphs (identified with their edge
sets) on the vertex set
 with covering
number at most p (equivalently, with independence number
at least
with covering
number at most p (equivalently, with independence number
at least
 .
For
.
For
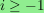 ,
I show that the rank
of the i-th homology group of
,
I show that the rank
of the i-th homology group of
 .
My proof takes place in a more general
setting where I consider complexes of hypergraphs.
In addition, I show that the
.
My proof takes place in a more general
setting where I consider complexes of hypergraphs.
In addition, I show that the
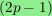 -skeleton of
-skeleton of
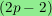 -connected.
For
-connected.
For
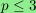 ,
I give a complete description of the
homology groups of
,
I give a complete description of the
homology groups of
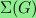 consisting of all
graphs on V that are contained in a graph isomorphic to
G. This document contains a list of all nontrivial complexes
of this kind on a vertex set of size
4, 5, or 6.
More precisely, for each nontrivial isomorphism
class
consisting of all
graphs on V that are contained in a graph isomorphic to
G. This document contains a list of all nontrivial complexes
of this kind on a vertex set of size
4, 5, or 6.
More precisely, for each nontrivial isomorphism
class
 of graphs, I have computed the homology of the
associated complex
of graphs, I have computed the homology of the
associated complex
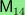 on 14 vertices.
Combining our observation with results due to Bouc
and to Shareshian and Wachs, I
conclude that the case
on 14 vertices.
Combining our observation with results due to Bouc
and to Shareshian and Wachs, I
conclude that the case
 is exceptional; for all other n,
the torsion subgroup of the bottom nonvanishing homology group
has exponent three or is zero.
The possibility remains that there is other torsion than
3-torsion in higher-degree homology groups of
is exceptional; for all other n,
the torsion subgroup of the bottom nonvanishing homology group
has exponent three or is zero.
The possibility remains that there is other torsion than
3-torsion in higher-degree homology groups of
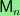 when
when
 and
and
 .
.
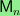 , which
is the simplicial complex of
matchings in the complete graph
, which
is the simplicial complex of
matchings in the complete graph
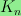 .
Combining these sequences in
different ways, I prove several results about the
3-torsion part of the homology of
.
Combining these sequences in
different ways, I prove several results about the
3-torsion part of the homology of
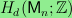 whenever
whenever
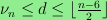 , where
, where
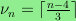 .
By a theorem due to Bouc and to Shareshian and Wachs,
.
By a theorem due to Bouc and to Shareshian and Wachs,
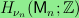 is a
nontrivial elementary 3-group for almost all n and the
bottom nonvanishing homology group of
is a
nontrivial elementary 3-group for almost all n and the
bottom nonvanishing homology group of
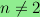 .
Second, I prove that
.
Second, I prove that
 .
Third, for each
.
Third, for each
 , I show
that there is a polynomial
, I show
that there is a polynomial
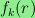 of
degree 3k such
that the dimension of
of
degree 3k such
that the dimension of
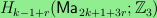 ,
viewed as a vector space
over
,
viewed as a vector space
over
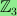 ,
is at most
,
is at most
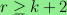 .
.
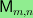 , which is the simplicial complex of
matchings in the complete bipartite graph
, which is the simplicial complex of
matchings in the complete bipartite graph
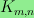 .
First, I demonstrate that there is nonvanishing
3-torsion in
.
First, I demonstrate that there is nonvanishing
3-torsion in
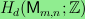 whenever
whenever
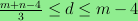 and
whenever
and
whenever
 and
and
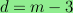 .
Combining this result with theorems due to
Friedman and Hanlon and to Shareshian and Wachs,
I characterize all triples
.
Combining this result with theorems due to
Friedman and Hanlon and to Shareshian and Wachs,
I characterize all triples
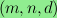 satisfying
satisfying
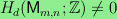 .
Second, for each
.
Second, for each
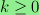 ,
I show that there is a polynomial
,
I show that there is a polynomial
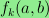 of degree 3k such that
the dimension of
of degree 3k such that
the dimension of
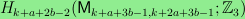 ,
viewed as a vector space over
,
viewed as a vector space over
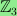 ,
is at most
,
is at most
 and
and
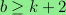 .
In addition, I give the first
computer-free proof that
.
In addition, I give the first
computer-free proof that
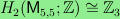 . Several proofs are based on a new long
exact sequence relating the homology of a certain subcomplex of
. Several proofs are based on a new long
exact sequence relating the homology of a certain subcomplex of
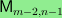 and
and
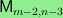 .
.
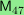 and 13-torsion in the homology of
and 13-torsion in the homology of
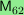 .
Finally, I compute the ranks of the 3- and 5-subgroups
of
.
Finally, I compute the ranks of the 3- and 5-subgroups
of
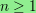 and δ ≥ 1, I examine the simplicial
complex of graphs on n vertices in which each vertex has degree
at most δ;
one identifies a given graph with its edge set and
admits one loop at each vertex.
and δ ≥ 1, I examine the simplicial
complex of graphs on n vertices in which each vertex has degree
at most δ;
one identifies a given graph with its edge set and
admits one loop at each vertex.
 yields the matching complex, and it is known that
there is 3-torsion in degree d of the homology of this complex
whenever
yields the matching complex, and it is known that
there is 3-torsion in degree d of the homology of this complex
whenever
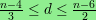 .
I establish similar bounds for δ ≥ 2.
Specifically,
there is 3-torsion in degree d whenever
.
I establish similar bounds for δ ≥ 2.
Specifically,
there is 3-torsion in degree d whenever
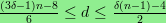 . The situation for other pairs
(d,n) remains unknown in general. To detect
torsion, I construct an explicit cycle z that is easily
seen to have the property that 3z is a boundary. Defining a
homomorphism that sends z to a non-boundary element in the
chain complex of a certain matching complex, I obtain that z
itself is a non-boundary. In particular, the homology class of
z has exponent 3.
. The situation for other pairs
(d,n) remains unknown in general. To detect
torsion, I construct an explicit cycle z that is easily
seen to have the property that 3z is a boundary. Defining a
homomorphism that sends z to a non-boundary element in the
chain complex of a certain matching complex, I obtain that z
itself is a non-boundary. In particular, the homology class of
z has exponent 3.
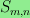 be the graph on the vertex set
be the graph on the vertex set
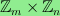 with an edge between
with an edge between
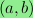 and
and
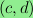 if
and only if either
if
and only if either
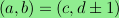 or
or
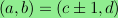 modulo
modulo
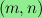 .
I consider the simplicial complex
.
I consider the simplicial complex
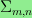 .
of independent sets in
.
of independent sets in
 are roots of unity,
where
are roots of unity,
where
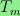 is a certain "transfer matrix"
associated to
is a certain "transfer matrix"
associated to
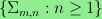 . In the language of statistical mechanics, the
reduced Euler characteristic of
. In the language of statistical mechanics, the
reduced Euler characteristic of
 .
.
 with the property that
with the property that
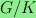 is finite.
I examine the homology of the independence complex
is finite.
I examine the homology of the independence complex
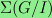 of
of
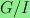 for subgroups I of K of full rank, focusing on
the case that G is the square, triangular, or hexagonal grid.
Specifically, I look for a certain kind of homology cycles referred
to as ``cross-cycles'', the rationale for the
terminology being that they
are fundamental cycles of the boundary
complex of some cross-polytope.
For the special cases just mentioned, I determine the set
for subgroups I of K of full rank, focusing on
the case that G is the square, triangular, or hexagonal grid.
Specifically, I look for a certain kind of homology cycles referred
to as ``cross-cycles'', the rationale for the
terminology being that they
are fundamental cycles of the boundary
complex of some cross-polytope.
For the special cases just mentioned, I determine the set
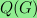 of rational numbers r such that there is a group I with the
property that
of rational numbers r such that there is a group I with the
property that
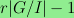 ;
;
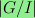 denotes the size of the vertex set of
denotes the size of the vertex set of
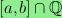 .
For example, for the square grid, one obtains the interval
.
For example, for the square grid, one obtains the interval
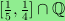 .
.
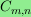 be the graph on the vertex set
be the graph on the vertex set
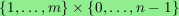 in which there is an edge between
in which there is an edge between
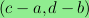 is an integer linear combination of the two vectors
is an integer linear combination of the two vectors
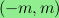 and
and
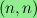 . I examine the
reduced Euler characteristic
. I examine the
reduced Euler characteristic
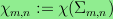 , where
, where
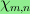 for fixed
m depends on the divisibility of m by
three. Specifically, if m is not
divisible by three, then
for fixed
m depends on the divisibility of m by
three. Specifically, if m is not
divisible by three, then
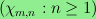 is periodic.
If m is divisible by three, then
is periodic.
If m is divisible by three, then
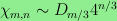 for large n, where
for large n, where
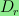 equals the number of
orbits under cyclic rotation of the set of all periodic sequences
of length 2r with r zeros and r ones.
The proof is based on results from
equals the number of
orbits under cyclic rotation of the set of all periodic sequences
of length 2r with r zeros and r ones.
The proof is based on results from  such that
such that
 is a face of Σ, the order being
given by subword inclusion. I prove that the order complex of
Γ(Σ) has the same Euler characteristic as the order
complex of the Rees product of the face poset of Σ and an
n-chain.
In particular, I settle a conjecture due to Björner and Welker,
stating that the two order complexes are homotopy equivalent.
Shareshian and Wachs discovered another proof of the conjecture
independently of my work.
is a face of Σ, the order being
given by subword inclusion. I prove that the order complex of
Γ(Σ) has the same Euler characteristic as the order
complex of the Rees product of the face poset of Σ and an
n-chain.
In particular, I settle a conjecture due to Björner and Welker,
stating that the two order complexes are homotopy equivalent.
Shareshian and Wachs discovered another proof of the conjecture
independently of my work.