Nivåkurvor för några konjugerat harmoniska funktioner

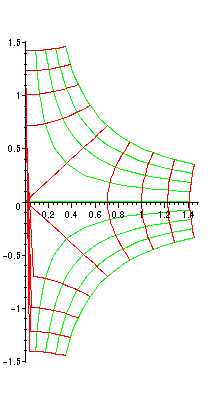
Vi börjar med funktionen z² = x² - y² + i2xy.

Här finns alltså två harmoniska funktioner u(x,y) = x² - y² och v(x,y) = 2xy vars nivåkurvor (röda för u, gröna för v) visas här nedan:

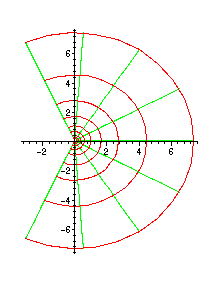
Nu studerar vi log z = ln + i arg z, vars konjugerade harmoniska funktioner är
u(x,y) = ln(x²+y²)^1/2 och v(x,y) = (x,y),

(arg z = (x,y) kan uttryckas med hjälp av arctan-funktionen. Man får dock olika uttryck i olika kvadranter)

Nivåkurvorna blir i detta fall cirklar (u(x,y) = C) resp. räta linjer genom origo (v(x,y) = C).

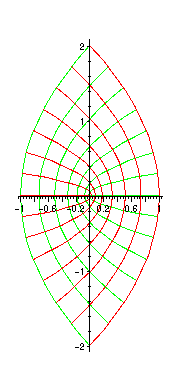
Slutligen betraktar vi funktionen z^1/2 som efter litet räkningar kan visas ha

realdelen u(x,y) = ((r + x)/2)^1/2 och

imaginärdelen v(x,y) = ((r-x)/2)^1/2 , där r = (x²+y²)^1/2.

(Räkna gärna själv. Använd polära koordinater!)

Efter ytterligare litet räkningar visar det sig att nivåkurvorna u(x,y) = C och v(x,y) = C kan skrivas

x = -(y² - 4C⁴)/4C²          resp.          x = (y² - 4C⁴)/4C².

Man ser att kurvorna är liggande, motriktade parabler.

Här nedan finns de plottade (u=C röda, v=C gröna).