Trigonometrins utveckling
Trigonometrins historia är lång och ganska svår att följa eftersom den länge uppfattades som en del av den rena geometrin och därför att den matematiska notationens bristande utveckling inte tillät formuleringen av det vi nu kallar trigonometriska formler. De antika matematiker som sysslade med hithörande frågor var tvungna att beskriva sina beräkningar med ord vilket naturligt hindrade uppkomsten av en effektiv kalkyl. Två namn som brukar nämnas i samband med tidig trigonometri är Hipparkos (100-talet f.Kr.) och Ptolemaios (c.a 68 - 165 e.Kr.).Trigonometrin undergick en fantastisk utveckling efter införandet av matematisk notation och det matematiska funktionsbegreppet.
En märklig upptäckt gjordes efter införande av de komplexa talen (z=x+iy, där i2=-1)
och av funktioner av komplexa tal.
Det visade sig att exponentialfunktionen ex och de trigonometriska cosx och sinx
stod i ett tidigare dolt förhållande till varandra.
Detta uttrycks av den s.k. Eulers formel:
(Leonhard Euler, 1700-talet).
Om man där sätter x =
får man ett samband mellan de fem viktigaste talen inom matematiken, e, i ,
, 1 och 0 :
En senare oerhört viktig uppfinning är ju naturligtvis
Fourierserierna, som ju kan sägas utgöra en gren av trigonometrin eftersom de vanligen består av trigonometriska funktioner.
Fourierserierna beskriver alltså vågrörelser med som en summa av svängningar med olika frekvens och amplitud:
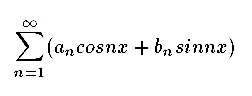
Fourier införde dem i samband med studium av värmeledning i början av 1800-t