4C. Napiers och Briggs logaritmerFöre datorernas tid innebar de en ofantlig förenkling av numeriska beräkningar. Enligt Lapalce (1749-1827) fördubblade de livslängden för en astronom genom att förkorta arbetet. Med hjälp av logaritm-tabeller kunde man ersätta tidskrävande multiplikationer av flersiffriga tal med mindre krävande additioner. Principen var enkel. Den byggde på sambandet log (AB) = log A + log B. (Den vanligaste logaritmen var den briggska som hade talet 10 som bas). Ville man multiplicera talen A och B gick man in i en logaritmtabell och fick fram talen log A och log B. Därefter adderade man dessa tal och fick därmed, p.g.a. logaritmens egenskaper, talet log(AB). Slutligen gick man in i logaritmtabellen och fick, genom att använda tabellen i omvänd ordning, ut det sökta talet AB. Även räknestickan, civilingenjörernas klassiska bröstficksredskap,
bygger (byggde kanske, när såg någon senast en räknesticka?) på logaritmer.
Vi har talat något om att logaritmer kan ha olika baser.
Basen är ju det tal log x upphöjs till så att resultatet blir x.
Om basen är a visar man det genom beteckningen loga x. Ibland behöver man byta bas på en logaritm. Här är formeln:
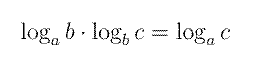 Vill man byta bas från a till b får man alltså använda faktorn loga b: Observera också att om man sätter c = a i formeln får man det intressanta sambandet Exempelvis: ln 10 = 1/log10e. |