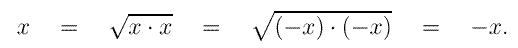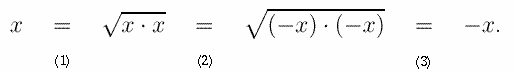3B : Logiken i ekvationslösningen.

Ekvationen (1) (x-3)(x-2) = 0 med lösningen: (2) x=3 eller x=2
kan jämföras med problemet eller egenskapen (1') "x är plåtslagare och bor i Söderbyn" med lösning (2') "x är Evert Persson eller Ulf Modin".

I båda fallen strävar man efter att efter vissa slutledningar formulera om ekvationerna/egenskaperna så att man slutligen kommer fram till en eller flera lösningar.

Dessa omformuleringar är i bästa fall ekvivalenta med de tidigare, dvs de har samma lösningsmängd (objekt som har egenskapen ifråga).
Men ibland (exempelvis när man kvadrerar en ekvation) får man nöja sig med att en ekvation/egenskap medför nästa ekvation/egenskap.

Antag att p(x) och q(x) är två egenskaper hos x och att P och Q är motsvarande mängder av objekt som har respektive egenskaper.
Dessa egenskaper kan exempelvis vara två ekvationer och P och Q motsvarande lösningsmängder.

p(x) <=> q(x) betyder att de båda egenskaperna är ekvivalenta vilket innebär att mängderna P och Q är desamma, P=Q.

Om man istället endast vet att p(x) medför ( implicerar ) q(x), skriver man
p(x) => q(x). Då gäller att P är en delmängd till Q,
vilket skrivs P Q.
Observera att en mängd alltid räknas som en av delmängderna till sig själv.

Slutsatsen av ovanstående är att om ekvationerna i en lösning inte alla är ekvivalenta utan i något fall består av två ekvatoioner där den föregående endast medför den efterföljande, så utökas lösningsmängden och man blir tvungen att pröva de erhällna rötterna i ursprungsekvationen.

Här ett exempel på samspelet mellan logiken i ekvationslösningen och lösningsmängdernas storlek.
Den ursprungliga ekvationen saknar faktiskt lösning, men lösningsmängderna växer här vid varje kvadrering.

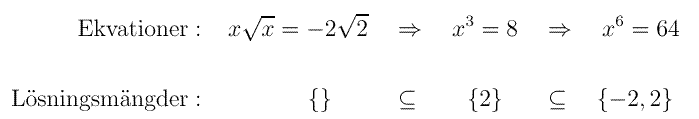Det är alltså inte fel att ha ickeekvivalenta ekvationer i en ekvationslösning, bara implikationspilarna går åt rätt håll: => . Den slutliga prövningen ser då ändå till att lösningen blir den korrekta.
Däremot är det farligt om pilen går åt fel håll : <=.
Då riskerar man nämligen att tappa någon eller några rötter. Exempel:

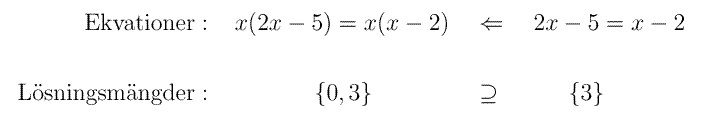Divisionen med x i bägge led ledde alltså till att roten x=0 försvann.
Notera att det är den andra ekvationen som medför den första.

Slutsatsen är alltså att i sådana här fall måste varje bortförkortad faktor studeras närmare. Den kan svara mot en rot till ekvationen.