Denna vecka fortsätter vi med egenvärden och egenvektorer:

7.2 Diagonalization

samt avslutar detta område (och kursen!) med följande geometriska tillämpningar:

9.6 Diagonalizing Quadratic Forms; Conic Sections.

9.7 Quadric Surfaces

7.2 Diagonalization I föregående avsnitt visades exempel på att en nxn-matris A hade n st. linjärt oberoende vektorer, men det fanns också exempel på att detta antal var mindre. Sådana olika fall finns också i Inlämningsuppgiften. I avsnitt 7.2 formuleras detta som Egenvektorproblemet: Existerar det n st. linjärt oberoende egenvektorer till nxn-matrisen A? Detta problem visar sig vara relaterat till Diagonaliseringsproblemet: Finns det en inverterbar matris P som diagonaliserar nxn-matrisen A, så att P-1AP blir en diagonalmatris ? Om A är diagonaliserbar existerar alltså diagonalmatrisen D = P-1AP som har liknande egenskaper som A, bl.a. har A och D samma egenvärden. Thm 7.2.1. utsäger helt enkelt att egenvektorproblemet och diagonaliseringsproblemet är ekvivalenta. Dvs. om (a)    A har n st. linjärt oberoende egenvektorer,    så gäller (b)    A är diagonaliserbar, och omvänt: Om (b) så (a). Det är en utmärkt övning att försöka följa beviset av denna sats. Kärnpunkten är observationen att om P har kolumnvektorerna p1, p2, ...,pn, så har produktmatrisen AP kolumnerna Ap1, ..., Ap1. Antag nu att (a) gäller och definiera P som en matris som har A:s egenvektorer pj (med motsv. egenvärden j ) som kolumner. Då gäller ju Apj = jpj , vilket visar att AP har kolumnerna jpj. Detta leder till slutsatsen att AP = PD och alltså P-1AP = P-1PD = D. dvs. (b). På likartat sätt visas att (b) medför (a). (Se s.365-366 för mer detaljer). På s. 367 beskrivs metoden att diagonalisera en matris A i tre steg: Steg 1. Bestäm n st. linjärt oberoende egenvektorer p1, p2, ...,pn till A med motsvarande egenvärden 1, 2, ... ,n. ( Finns det inte så många egenvektorer blir alltså slutsatsen att A inte är diagonaliserbar.) Steg 2. Bilda matrisen P som har vektorerna p1, p2, ...,pn som kolumner. Steg 3. Den sökta diagonaliserade matrisen är då D = P-1AP, där D:s diagonalelement är egenvärdena 1, 2, ... ,n. Ex. 1, 2, s.367-368, är utmärkta exempel på diagonaliseringar av 3x3-matriser där matrisen i båda fallen har ett enkelt och ett dubbelt egenvärde. I Ex. 1 finns det tre linjärt oberoende egenvektorer varför diagonalisering är möjlig. I Ex.2 däremot finns bara två linjärt oberoende egenvektorer och därmed är diagonalisering inte möjlig. För diagonaliseringsproblemet är det alltså väsentligt att veta om det går att hitta maximalt antal linjärt oberoende egenvektorer. Thm 7.2.2 ger ett viktigt tillräckligt villkor för detta: Om egenvektorerna v1, v2, ...,vn svarar mot inbördes olika egenvärden är dessa egenvektorer linjärt oberoende. Slutsatsen kommer direkt i Thm 7.2.3: Om nxn-matrisen A har n st. olika egenvärden är A diagonaliserbar. Om egenvärdena är olika går det alltså bra att diagonalisera. Om något egenvärde är multipelt kan det däremot som vi har sett bli problem. För diskussionen av hithörande frågor införs på s. 371 begreppen geometrisk multiplicitet och algebraisk multiplicitet för ett visst egenvärde . Den geometriska multipliciteten är antalet linjärt oberoende egenvektorer som svarar mot egenvärdet i fråga, medan den algebraiska multipliciteten anger multipliciteten hos som rot till den karakteristiska ekvationen. Är en dubbelrot är alltså den algebraiska multipliciteten = 2. Thm 7.2.4 beskriver relationen mellan dessa multipliciteter: (a)   För ett visst egenvärde är den geometriska multipliciteten alltid mindre eller lika med den algebraiska . (b)   A är diagonaliserbar om och endast om de båda multipliciteterna är lika för varje egenvärde. Avsnittet slutar med en tillämpning av diagonalisering: Beräkning av matrispotenser Ak för diagonaliserbara matriser A. Principen är enkel och framgår redan i fallet k=2: (P-1AP)2 = P-1APP-1AP = P-1AIAP-1 = P-1A2P. Om nu P-1AP = D, diagonalmatris, får man att D2 = P-1A2P, vilket ju innebär att A2 = PD2P-1 På samma sätt visas att Ak = PDkP-1 för varje naturligt tal k. Poängen med denna formel är naturligtvis att det är så mycket lättare att beräkna potenser av diagonalmatriser D än av andra matriser A. Satser och begrepp Egenvektorproblemet Diagonaliseringsproblemet Thm 7.2.1: De båda problemen är ekvivalenta. Att diagonalisera en matris (steg 1 - steg 3) Thm 7.2.2-3: Om A:s egenvärden är olika är A:s egenvektorer linjärt oberoende och A är alltså diagonaliserbar. Geometrisk multiplicitet hos egenvärde Algebraisk multiplicitet hos egenvärde Thm 7.2.4:Geometrisk multiplicitet algebraisk multiplicitet. Formeln Ak = PDkP-1 Hemuppgifter 4 6 8 11 12 19 20a

9.6 Diagonalizing Quadratic Forms; Conic Sections. Detta avsnitt utgör en tillämpning av diagonaliseringsmetoden som behandlades i 7.2. Dock bygger det något på stoff som formellt inte tillhör kursen. Detta bör man känna till: En kvadratisk form är ett variabeluttryck av enbart andragradstermer som alltså kan definieras av ett uttryck av typen xTAx där variablerna är komponenterna i vektorn xT = [x1 x2 ... xn] och A en symmetrisk nxn-matris. Kontrollera gärna själv att matrisprodukten xTAx då xT= [ x1     x2 ] och 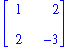A =     blir    x12 + 2x1x2 + 2x2x1 - 3x22    =    x12 + 4x1x2 - 3x22 . Andra exempel finns på s. 475. Från 7.3 behöver man också känna till något om symmetriska matrisers egenvektorer. (En symmetrisk matris A uppfyller A = AT och är alltså symmetrisk med avseende på diagonalen, Ajk = A kj). Thm 7.3.1 hävdar bland annat att om A är en symmetrisk nxn-matris så har A n st. ortonormerade egenvektorer och är därmed ortogonalt diagonaliserbar. En mängd ortonormerade vektorer är alla inbördes ortogonala och har längden = 1. 'Ortogonalt diagonaliserbar' innebär att A är diagonaliserbar av en ortogonal matris, dvs av en matris vars kolumner (och därmed även rader) är ortonormerade. För en ortogonal matris P gäller PT = P-1, vilket innebär att PTP = I som i sin tur leder till att det(P) = +1 eller -1. Geometriskt sett definierar ortogonala matriser transformationer som kan beskrivas som stela vridningar (+ev speglingar) och som lämnar de transformerade vektorernas längder oförändrade. Nu åter till avsnitt 9.6. Thm 9.6.1 beskriver hur diagonaliseringstekniken från kapitel 7 kan användas till att avlägsna blandade termer (= icke-kvadrattermer) från kvadratiska former. Närmare bestämt: Låt xTAx vara en kvadratisk form där matrisen A alltså är symmetrisk. Därmed finns det en ortogonal matris P, som diagonaliserar A, dvs D = P-1AP = PTAP = den diagonala matris som har A:s egenvärden som diagonalelement. (Notera att P-1 = PT eftersom P är ortogonal.) Genom substitutionen x = Py utförs denna diagonalisering även på den kvadratiska formen: x = Py ger : xTAx = (Py)TAPy = yTPTAPy =yTDy, vilket är en kvadratisk form med enbart kvadrattermer. (Här ovan användes den användbara relationen (AB)T = BTAT.) Därefter behandlas i 9.6, med viss utförlighet, de s.k koniska sektionerna, dvs de plana kurvor som uppstår då en kon (egentligen en dubbelkon dvs. två koner med samma centralaxel och med motriktade spetsar) snittas av ett plan. Beroende på planets vinkel med centralaxeln får man tre sorters kurvor: ellipser, parabler och hyperbler. En parabel utgör gränsfallet mellan ellipserna och hyperblerna och erhålles då det snittande planet är parallellt med en av konens sidlinjer. Ekvationerna för dessa kurvor är alltid polynomekvationer av andra graden. Om kurvornas symmetriaxlar lutar i förhålande till x- och/eller y-axeln förekommer den blandade termen 'xy' i ekvationen. Det blir alltså ett diagonaliseringsproblem att finna en substitution som får denna xy-term att försvinna. Geometriskt innebär detta att man vrider koordinatsystemet så att någon av kurvans symmetriaxlar blir parallell med x- eller y-axeln. På s. 489-490 redogörs för en diagonaliseringsmetod som i stort sett är analog med den som behandlades i 7.2. Dock finns en liten finess här som inte har någon motsvarighet i 7.2: När man har funnit två ortonormerade egenvektorer till A (som svarar mot kurvans associerade kvadratiska form) ska man alltså enligt den allmänna metoden bilda den diagonaliserande matrisen P med egenvektorerna som kolumner. Ordningen mellan dessa kolumner föreskrivs inte. Men här anges det (Steg 2 s. 490) att man skall väja kolumnernas ordningsföljd så att det(P) blir =1. (Detta är alltid möjligt). Därmed svarar substitutionen x = Py mot en ren rotation. I fallet det(P) = -1 svarar substitutionen i stället mot en rotation + en spegling. Med denna nya restriktion kan man hävda, vilket görs i Thm 9.6.2 (Principalaxelsatsen), att diagonaliseringen utförs med enbart en rotation. Satser och begrepp En del fakta om kvadratiska former symmetriska matrisers egenvektorer ortonormerade egenvektorer ortogonala matriser ingår inte i kursen, men har samlats härovan för att underlätta inläsningen. Thm 9.6.1: En kvadratisk form xTAx kan diagonaliseras genom en substitution x = Py (P ortogonal) till yTDy, där D = PTAP Konisk sektion Ekvationens associerade kvadratiska form Diagonaliseringsmetoden (Steg 1 - Steg 3, s. 489 - 490) Obs det(P) = +1 Thm 9.6.2 (Principalaxelsatsen): De koniska sektionerna kan diagonaliseras med enbart en rotation. Hemuppgifter 6bcfg 7b 8a 11

9.7 Quadric Surfaces Detta avsnitt behandlar andragradsytor i R3 på samma sätt som avsnitt 9.6 behandlar andragradskurvor i R2. Fig. 1 på s. 496 ger en utmärkt översikt över de sex viktigaste typerna av andragradsytor. Dessa är alltså: Ellipsoid Enmantlig hyperboloid (Hyperboloid of one sheet) Tvåmantlig hyperboloid (Hyperboloid of two sheets) Elliptisk kon Elliptisk paraboloid Hyperbolisk paraboloid eller Sadelyta I övrigt presenteras samma teori som i 9.6 om diagonalisering av ytornas associerade kvadratiska former. Metoden anges på s. 497 inklusive föreskriften att den diagonaliserande ortogonala matrisen ska ha determinanten = 1. Thm. 9.7.1 formulerar motsvarande principalaxelteorem som anger att diagonaliseringen kan åstadkommas av en ortogonal matris med determinanten = 1. Satser och begrepp De olika typerna av andragradsytor (Fig.1, s. 496) Diagonaliseringsmetoden (s. 497) Thm. 9.7.1 (Principalaxelteoremet för andragradsytor) Hemuppgifter 6d 8